- квадратное уравнение относительно p; в принципе можно решать с дискриминанта, но числа не самые простые, поэтому идти по этому пути лень. Пытаемся угадать одно из решений и без труда его находим: p=1. Дальнейшее элементарно: по теореме Виета произведение корней равно 28-4x, а раз первый корень p=1, то второй равен p=28-4x.
1-й случай
2-й случай.
Решение x= 3 легко угадывается (8=8), других решений быть не может, поскольку функция, стоящая в левой части уравнения, возрастает, а функция, стоящая в правой части уравнения, убывает.
k≠0
График пересекает ось OX⇒в точке пересечения y=0
Решаем уравнение: lgkx-2lg(x+1)=0⇒lgkx=2lg(x+1)⇒lgkx=lg(x+1)^2⇒
kx=(x+1)^2⇒x^2+2x+1=kx⇒x^2+x*(2-k)+1=0
Квадратное уравнение имеет единственное решение, если дискриминант равен 0.
D=b^2-4ac=(2-k)^2-4=0⇒(2-k)^2=4⇒
2-k=2⇒k=0 - не входит в ОДЗ
2-k=-2⇒k=4
ответ: k=4
Решим уравнение x^(lgx)-100000x^4=0⇒x^(lgx)=100000x^4
ОДЗ: x>0
Прологарифмируем обе части уравнения по основанию 10:
lgx*lgx=lg100000+lgx^4⇒lg^2(x)=5+4lgx⇒lg^2(x)-4lgx-5=0
Замена: lgx=t⇒t^2-4t-5=0⇒по теореме Виетта
t1+t2=4; t1*t2=-5⇒t1=5; t2=-1⇒
lgx=5⇒x1=10^5=100000
lgx=-1⇒x2=10^(-1)=0,1
домножим уравнение на 4 и сделаем замену 2t=p>0:
1-й случай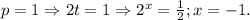
2-й случай.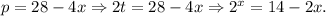
Решение x= 3 легко угадывается (8=8), других решений быть не может, поскольку функция, стоящая в левой части уравнения, возрастает, а функция, стоящая в правой части уравнения, убывает.
ответ: - 1; 3