Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
sladkoe102
27.05.2021 12:20 •
Алгебра
Определите количество корней уравнения sin2 x = √2cos x на промежутке [0; 2π)
Показать ответ
Ответ:
kisylay85
25.05.2020 19:02
V
k є Z
n є Z
из них на промежутке [0;2π) это корни
т.е. 4 корня
ответ: 4 корня
0,0
(0 оценок)
Популярные вопросы: Алгебра
ВИТ21
09.03.2023 00:18
Найдите значение выражения 5a^2-5ax-7a+7x при a=4; x=-3...
Mara1111176
20.06.2021 23:05
найдите целую часть числа (√n+√(n+1))^2, n - натуральное число....
Makarzzz
28.12.2021 09:12
Определите четность функции y=sin3x, y=xsin5x, y=x^3-sin2x, y=|sin9x|. определите период функции y=sin x/2, y=2cos3x,y=2-3tgx решите неравенство 1+2cos больше или равно...
Влад27128
28.12.2021 09:12
Вычислите координаты точек в которых прямая y=0,5х + 1 пересекает оси кординат и постройте эту прямую...
artiom726
15.03.2022 15:48
Разложите на множители а)5а-5в+с(а-в) б)а^3-а^2-4а+4 в)25в^2-(в-5)^2...
elenanatalja
25.10.2022 13:42
Периметр равнобедренного треугольника равен 53 см.найдите стороны этого треугольника , если боковая сторона на 5 см меньше основания....
aidafarhadova
25.10.2022 13:42
Преобразуйте в множители стандартного вида а)(5х-у)(5х-у) б)(а+4)^2-2а(а-3)...
qwetdfgdsa
25.10.2022 13:42
Решите неравенство , 6х-7 7х+8...
Лизка250515
14.11.2021 20:47
С8 класс. освободитесь от иррациональности в знаменателе дроби. 10 4 - 2£3 £- я так обозначила квадратный корень...
Bublick08
14.11.2021 20:47
Угол авс , ас равен вс равен 5, угол а равен 45 грдусов. найти s abc? решить с рисунком если можно?...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
из них на промежутке [0;2π) это корни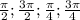
т.е. 4 корня
ответ: 4 корня