Определите количество решений системы графическим методом: {x+y = -2 {3x-y = 6 Запишите алгоритм построения заданных графиков и подпишите их при построении.
1) ОДЗ: 20х+15 >0 ⇒ x>-0,75 Логарифмическая функция с основанием 0,7 монотонно убывает и каждое свое значение принимает только в одной точке. Поэтому если логарифмы равны, то и аргументы равны 20х+15=5·17 20х+15=85 20х=70 х=3,5 - входит в ОДЗ ответ. 3,5 2) ОДЗ: 9х+6 > 0 ⇒ x>-2/3 9x+6=51 9x=51-6 9x=45 x=5 - входит в ОДЗ ответ. 5 3) ОДЗ: 12х+8>0 ⇒ x>-2/3 12x+8=4·20, 12x+8=80, 12x=72 x=6 - входит в ОДЗ ответ. 6 4) ОДЗ х>0 Применяем основное логарифмическое тождество 1,8 входит в ОДЗ ответ. 1,8 5) ОДЗ: 2х+5>0 ⇒ x>-2,5 -1,5 входит в ОДЗ ответ. -1,5
Рисунок смотрите в приложении (на нем изображены равные векторы).
Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).
а). Векторы и равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен градусов (получаем, что это коллинеарные, но не равные векторы).
.
б). Векторы и равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
.
в). Векторы и опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата - градусов).
Логарифмическая функция с основанием 0,7 монотонно убывает и каждое свое значение принимает только в одной точке. Поэтому если логарифмы равны, то и аргументы равны
20х+15=5·17
20х+15=85
20х=70
х=3,5 - входит в ОДЗ
ответ. 3,5
2) ОДЗ: 9х+6 > 0 ⇒ x>-2/3
9x+6=51
9x=51-6
9x=45
x=5 - входит в ОДЗ
ответ. 5
3) ОДЗ: 12х+8>0 ⇒ x>-2/3
12x+8=4·20,
12x+8=80,
12x=72
x=6 - входит в ОДЗ
ответ. 6
4) ОДЗ х>0
Применяем основное логарифмическое тождество
1,8 входит в ОДЗ
ответ. 1,8
5) ОДЗ: 2х+5>0 ⇒ x>-2,5
-1,5 входит в ОДЗ
ответ. -1,5
Рисунок смотрите в приложении (на нем изображены равные векторы).
Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).а). Векторы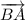 и
и 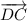 равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен
равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен 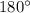 градусов (получаем, что это коллинеарные, но не равные векторы).
градусов (получаем, что это коллинеарные, но не равные векторы).
б). Векторы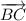 и
и 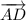 равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
в). Векторы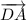 и
и 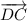 опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата -
опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата - 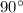 градусов).
градусов).
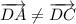
ответ:а) нет;
б) да;
в) нет.