Определите знаменатель бесконечно убывающей геометрической прогрессии, если сумма ее членов с нечетными номерами вдвое больше, чем сумма всех ее членов
Рассмотрим члены этой прогрессии с нечетными номерами. Это также геометрическая прогрессия с первым членом и знаменателем , причем геометрическая прогрессия бесконечно убывающая.
Сумма этой бесконечно убывающей геометрической прогрессии:
По условию эта сумма вдвое больше, чем предыдущая:
Пусть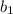 - первый член данной прогрессии, а
- первый член данной прогрессии, а 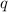 - ее знаменатель.
- ее знаменатель.
Тогда, сумма бесконечно убывающей геометрической прогрессии:
Рассмотрим члены этой прогрессии с нечетными номерами. Это также геометрическая прогрессия с первым членом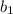 и знаменателем
и знаменателем 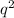 , причем геометрическая прогрессия бесконечно убывающая.
, причем геометрическая прогрессия бесконечно убывающая.
Сумма этой бесконечно убывающей геометрической прогрессии:
По условию эта сумма вдвое больше, чем предыдущая:
Поскольку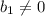 и
и 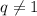 , то сократим:
, то сократим:
ответ: -1/2