В одном сосуде 49 л. воды, а во второй-36 л. Если долить доверху первую сосуд с другой, то вторая сосуд будет наполнена только наполовину; если же долить второй сосуд вверх с первой, то первая будет наполнена только на треть. Какая емкость каждого сосуда?
ответ: a ∈ (-∞; -25/21) ∪ (1; 25/8).
Объяснение:
Заметим, что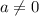
(т.к. при а = 0 данное уравнение преобразуется в линейный вид, что само собой имеет одно решение).
D = 25 - 8a
Квадратное уравнение имеет два различные корня, если D>0
25 - 8a > 0 ⇔ a < 25/8
Воспользуемся теоремой Виета:
Пусть 1/a = t, тогда получаем квадратное уравнение 25t² - 4t - 21 = 0
D = 16 + 2100 = 2116; √D = 46
t₁ = -0.84
t₂ = 1
Обратная замена:
1/a = -0.84 ⇔ a = -25/21
1/a = 1 ⇔ a=1
---------(-25/21)++++++++(0)+++++++++(1)------------
a ∈ (-∞; -25/21) ∪ (1;+∞)
С учетом существования корней, получим a ∈ (-∞; -25/21) ∪ (1; 25/8).
51 и 68
Объяснение:
В одном сосуде 49 л. воды, а во второй-36 л. Если долить доверху первую сосуд с другой, то вторая сосуд будет наполнена только наполовину; если же долить второй сосуд вверх с первой, то первая будет наполнена только на треть. Какая емкость каждого сосуда?
Составим уравнения:
49-х=1/2в
36-у=1/3а
Выразим емкость каждого сосуда:
а=36+х
в=49+у
Подставим значения в наши уравнения:
49-х=1/2(49+у)
36-у=1/3(36+х)
Из второго ур-я выразим у:
36-у=12+х/3
у=24 -х/3
Подставим в первое ур-е:
49-х=1/2(49+24-х/3))
49-х=24,5+12-х/6
49-24,5-12=х-х/6
12,5=5/6х
75=5х
х=15
Подставим значение в выражение у:
у=24 -15/3
у=24-5
у=19
Найдем емкость сосудов:
36+15=51
49+19=68