Отрезки ас и вd пересекаются в точке м, которая является их серединой, ∠свм=25, ∠мсв=40. докажите,что δамd=δcмв. найти угол а в δамd. запишите решение и ответ. *

1) Область определения: x ∈ (-∞; ∞).
2) Четность-нечетность:



Т.к.  и , то функция является функцией общего вида.
3) Точки пересечения с Ox. Решим исходное уравнение при y = 0. (метод решения: Виета-Кардано)
Получим один корень: x = 0.148 - абсцисса точки пересечения графка с осью Ox. Координаты точки: (0.148; 0)

Точка пересечения с Oy. Найдем y, подставив в уравнение x = 0. Получим: y = -5. Координаты точки: (0, -5).

4) Так как функция кубическая, то точек экстремума не имеет.

5) Первая производная.


2. Вторая производная.

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

Откуда точка перегиба:
x = 5/3

На промежутке: (-∞ ;5/3)

Значит, функция выпукла.

На промежутке (5/3; ∞)

Значит, функция вогнута. 

6) 


7(график в приложениях)

Как мог.. Работа объемная, конечно)

Дана функция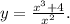

Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.

Приравняем её нулю ( при х не равном 0 можно только числитель).

x^3 - 8 = 0.

x^3 = 8,   х = ∛8 = 2. Это критическая точка.

С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).

На промежутках находим знаки производной.

Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.  

Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.

x =     -1         0         1          2           3

y' =  9      -         -7    0       0,7037.

• Минимум функции в точке: х = 2, у = 3.

• Максимума функции нет.

• Возрастает на промежутках: (-∞; 0) U (2; ∞).

• Убывает на промежутке: (0; 2).