Пусть весь путь S, а намеченная скорость v. Тогда 36% от пути это 0.36S , а 80% от скорости это 0,8v. Время которое водитель планировал затратить на весь путь равно: S/v Время которое водитель затратил на первую часть пути 0,36S/0.8v=0.45S/v Тогда на оставшиеся 0.64S пути ему остается S/v-0.45S/v=0.55S/v времени. Но водитель должен приехать на 5% быстрее, поэтому умножим полученный результат на коэффициент (1-0,05)=0,95. Тогда получим: 0.55S/v *0.95=0.5225S/v
Следовательно он должен двигаться со скоростью: 0.6S/(0.5225S/v)=1.22v
Примем начальный вклад за х, а начисляемый процент за у, тогда можем момтавить систему уравнений:
Оставим в левой части каждого уравнения х:
Первое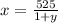
второе х*(1+2у)=540+200у
Уравняем правые части уравнений:
525*(1+2y)=(540+200y)*(1+y)
Находим корни квадратного уравнения. Получаем: у1=1,5 и у2=0,05
В случае у1=1.5 (или 150 % прибыли)
х=525/(1+у)=525/(1+1,5)=210 руб. - размер вклада
В случае у2=0,05 (или 5% прибыли)
х=525/(1+0,05)=500 руб. - размер вклада.
ответ: задача имеет два решения:
1) вклад 210 руб. под 150% годовых
2) вклад 500 руб под 5% годовых.
Пусть весь путь S, а намеченная скорость v. Тогда 36% от пути это 0.36S , а 80% от скорости это 0,8v.
Время которое водитель планировал затратить на весь путь равно: S/v
Время которое водитель затратил на первую часть пути 0,36S/0.8v=0.45S/v
Тогда на оставшиеся 0.64S пути ему остается S/v-0.45S/v=0.55S/v времени. Но водитель должен приехать на 5% быстрее, поэтому умножим полученный результат на коэффициент (1-0,05)=0,95. Тогда получим: 0.55S/v *0.95=0.5225S/v
Следовательно он должен двигаться со скоростью:
0.6S/(0.5225S/v)=1.22v
ответ: он должен увеличить скорость на 22%