Підсумкова контрольна робота
з алгебри у 9-А кл.

No1. Розв’яжіть систему нерівностей:
{

3x + 14 ≥ 4 − x ,
5x−1
4
−
x−1
2
≥ 3x − 2
.

No2. С ть вираз: (
x
x
2−25
−
x−8
x
2−10x+25) :
x−20
(x−5)
2
.
No3. При яких значеннях b і c вершина параболи
У=5x

2+bх+c знаходиться в т. В(2;7). Побудуйте

графік одержаної функції.
No4. Знайдіть периметр прямокутного трикутника,
якщо його площа становить 24 см кв., а довжина
гіпотенузи дорівнює 10 см.

внутренние 135° 150° 156°

внешние 45° 30° 24°

Объяснение:

Если n-угольник правильный, то все его углы равны между собой. Сумма всех внутренних углов n-угольника вычисляется по следующей формуле

S=180°(n-2), где n- количество углов, тогда один угол, будет равен отношению суммы всех углов к количеству, т.е. ∠=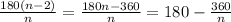. подставим вместо n искомые числа

n=8,∠=135°

n=12,∠=150°

n=15,∠=156°

Внешние углы, это углы, образующие с внутренним углом угол 180 градусов, а значит нужно вычесть от 180 величину внутреннего угла, т.е.

тогда

n=8,∠=45°

n=12,∠=30°

n=15,∠=24°

1) а) (a - 4)(a - 2) = a^2 - 6a + 8

б) (3x + 1)(5x - 6) = 15x^2 - 13x - 6

в) (3y - 2c)(y + 6c) = 3y^2 + 16cy - 12c^2

г) (b + 3)(b^2 + 2b - 2) = b^3 + 5b^2 + 4b - 6

2) а) 2x(a - b) + a(a - b) = (a - b)(2x + a)

б) 3x + 3y + bx + by = 3(x + y) + b(x + y) = (x + y)(3 + b)

3) 0,2y(5y^2 - 1)(2y^2 + 1) = (y^3 - 0,2y)(2y^2 + 1) =

= 2y^5 - 0,4y^3 + y^3 - 0,2y = 2y^5 + 0,6y^3 - 0,2y

4) а) 3x - xy - 3y + y^2 = x(3 - y) - y(3 - y) = (3 - y)(x - y)

б) ax - ay + cy - cx - x + y = a(x - y) - c(x - y) - (x - y) = (x - y)(a - c - 1)

5) Размеры клумбы: x и x+5 м.

Площадь дорожки 26 кв.м., а ширина 1 м. Дорожка показана на рис.

2x + 2(x+5) + 4 = 26

x + x + 5 + 2 = 13

2x = 13 - 7 = 6

x = 3 м - ширина клумбы.

x + 5 = 3 = 5 = 8 м - длина клумбы.