Простое число р при р>3 имеет вид р=6k+1 или p=6l-1, где k, l - некоторые натуральные числа
Поэтому либо делится на 12, так как множитель 12 делится на 12, а один из множителей k или 3k+1 делится на 2(если k четное, значит k - делится на 2, если k - нечетное, то 3k+1- четное и делится на 2)
либо
делится на 12, так как множитель 12 делится на 12, а один из множителей l или 3l-1 делится на 2(если l четное, значит l - делится на 2, если l - нечетное, то 3l-1- четное и делится на 2)
В обоих возможных случаях делится на 12*2=24. Доказано
Простое число р при р>3 имеет вид р=6k+1 или p=6l-1, где k, l - некоторые натуральные числа
Поэтому либо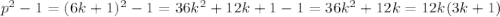 делится на 12, так как множитель 12 делится на 12, а один из множителей k или 3k+1 делится на 2(если k четное, значит k - делится на 2, если k - нечетное, то 3k+1- четное и делится на 2)
делится на 12, так как множитель 12 делится на 12, а один из множителей k или 3k+1 делится на 2(если k четное, значит k - делится на 2, если k - нечетное, то 3k+1- четное и делится на 2)
либо
В обоих возможных случаях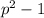 делится на 12*2=24. Доказано
делится на 12*2=24. Доказано