Чтобы найти точку пересечения прямых данной системы уравнений нужно перенести все члены каждого из уравнений в правую часть со сменой знака, а в левой части оставить переменную .
Теперь необходимо составить таблицу для переменных и , чтобы можно было подставлять значения выражений. После этого мы чертим координатную плоскость и находим точку пересечения прямых.
Затем можем приступать к координатной плоскости. По координатам в таблице чертим две прямые и рассматриваем точку, в которой они пересекаются. Остальное решение дано во вложении. Это приблизительная координата точки пересечения прямых.
метод подстановки.
Чтобы найти точку пересечения прямых данной системы уравнений нужно перенести все члены одного из уравнений в правую часть со сменой знака, а в левой части оставить переменную .
Теперь подставляем во первом уравнении вместо запись второго уравнения, а затем решим новое уравнение.
Это мы нашли значение переменной и в тоже время координату оси абсцисс для точки пересечения прямых. Теперь найдём координату оси ординат.
Запишем в ответ точную координату точки пересечения данных прямых.
Чтобы найти точку пересечения прямых данной системы уравнений нужно перенести все члены каждого из уравнений в правую часть со сменой знака, а в левой части оставить переменную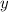 .
.
Теперь необходимо составить таблицу для переменных и
и 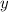 , чтобы можно было подставлять значения выражений. После этого мы чертим координатную плоскость и находим точку пересечения прямых.
, чтобы можно было подставлять значения выражений. После этого мы чертим координатную плоскость и находим точку пересечения прямых.
Затем можем приступать к координатной плоскости. По координатам в таблице чертим две прямые и рассматриваем точку, в которой они пересекаются. Остальное решение дано во вложении. Это приблизительная координата точки пересечения прямых.
метод подстановки.Чтобы найти точку пересечения прямых данной системы уравнений нужно перенести все члены одного из уравнений в правую часть со сменой знака, а в левой части оставить переменную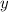 .
.
Теперь подставляем во первом уравнении вместо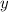 запись второго уравнения, а затем решим новое уравнение.
запись второго уравнения, а затем решим новое уравнение.
Это мы нашли значение переменной и в тоже время координату оси абсцисс для точки пересечения прямых. Теперь найдём координату оси ординат.
и в тоже время координату оси абсцисс для точки пересечения прямых. Теперь найдём координату оси ординат.
Запишем в ответ точную координату точки пересечения данных прямых.
ответ:sin^2t+cos^2t=1\\cos^2t=1-sin^2t\\cost=\pm\sqrt{1-sin^2t}
Т.к. t∈(π/2;π) - 2 четверть, в ней косинус отрицательный. значит перед корнем будет минус.
cost=-\sqrt{1-(\frac{5}{13})^2}=-\sqrt{\frac{169}{169}-\frac{25}{169}}=-\sqrt{\frac{144}{169}}=-\frac{12}{13}
sin2t=2sint*cost=2*\frac{5}{13}*(-\frac{12}{13})=-\frac{120}{169}cos2t=cos^2t-sin^2t=(-\frac{12}{13})^2-(\frac{5}{13})^2=\frac{144}{169}-\frac{25}{169}=\frac{119}{169}tg2t=\frac{sin2t}{cos2t}=\frac{-\frac{120}{169}}{\frac{119}{169}}=-\frac{120}{169}*\frac{169}{119}=-\frac{120}{119}ctg2t=\frac{1}{tg2t}=\frac{1}{-\frac{120}{119}}=-\frac{119}{120}