Пусть , где есть многочлен, каждый член которого входит в четной степени, а соответственно наоборот. Тогда из условия следует, что , откуда . Аналогично, , то есть числа являются корнями многочлена степени не выше 3. Противоречие. Стало быть, такого многочлена выделить нельзя, следовательно , то есть четная функция.
Пусть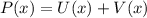 , где
, где 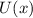 есть многочлен, каждый член которого входит в четной степени, а
есть многочлен, каждый член которого входит в четной степени, а 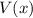 соответственно наоборот. Тогда из условия следует, что
соответственно наоборот. Тогда из условия следует, что 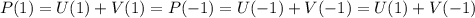 , откуда
, откуда 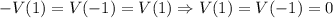 . Аналогично,
. Аналогично,  , то есть числа
, то есть числа 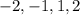 являются корнями многочлена
являются корнями многочлена 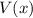 степени не выше 3. Противоречие. Стало быть, такого многочлена выделить нельзя, следовательно
степени не выше 3. Противоречие. Стало быть, такого многочлена выделить нельзя, следовательно 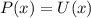 , то есть четная функция.
, то есть четная функция.