Ну, наччнем с того, что предположим, что сутки у них одинаковы по длительности и сутки состоят из целого числа часов, часы состоят из целого числа минут, минуты состоят из целого числа секунд.
Значит надо искать сомножители 715 - узнать вообще на сколько равных целых кусочков можно разделить это число: 715=5*11*13 получается, что возможны такие варианты: 715 минут - это 1) 5 суток по 11 часов, в каждом часе 13 минут 2) 5 суток по 13 часов, в каждом часе 11 минут 3) 11 суток по 5 часов, в каждом часе 13 минут 4) 11 суток по 13 часов, в каждом часе 5 минут 5) 13 суток по 5 часов, в каждом часе 11 минут 6)13 суток по 11 часов, в каждом часе 5 минут
по условию "минут в часе меньше, чем часов в сутках" - значит варианты 1, 3 и 5 не верны,
в оставшихся вариантах умножим часы на минуты - узнаем, сколько минут в сутках: на это число должно нацело делиться суточное к-во секунд - известные нам 1001:
5 суток по 13 часов, в каждом часе 11 минут - 143 минуты в сутках
11 суток по 13 часов, в каждом часе 5 минут - 65 минут в сутках
13 суток по 11 часов, в каждом часе 5 минут 55 минут в сутках
разложим на множители 1001 1001=7*11*13
вот они, знакомые 11*13 = 143 Получается, что только первый вариант имеет такие числа, чтобы суточное количество секунд нацело делилось на суточное к-во минут!
Итак, на планете Шелепука неделя состоит из 5 суток, сутки состоят из 13 часов, час состоит из 11 минут, минута состоит из 1001/143 = 7 секунд!
Исследуем знак второй производной: f''(x)=0 - когда где
Поскольку a³≤a², b³≤b², причем при a∈(0,1); b∈(0,1) неравенства строгие, делаем вывод, что такое возможно только при a=1; b=0 или a=0; b=1, при прочих a и b, удовлетворяющих второму уравнению, сумма их кубов будет меньше 1, откуда вторая производная всюду неотрицательна, то есть функция вогнута. А поскольку других решений на промежутке нет.
2) уравнение принимает вид
На этом участке подобное рассуждение не проходит; кроме x=2 точно есть корень слева от нуля, поскольку f(0)>6. Будем рассуждать иначе.
уравнение превращается в
Обе части положительны, смело возводим в квадрат (а можно было и к половинному углу свести):
6-6cos 2t-10sin 2t+2sin 2t cos 2t=0;
12sin² t-20 sin t cos t+4sin t cos t(cos² t-sin² t)=0; sin t=0 (⇒ a=0; b =2; x=2) или 3 sin t-5cos t+cos³ t-cos t sin² t=0;
(3sin t-5cos t)(cos²t+sin²t)+cos³ t-cos t sin^2 t=0;
3sin³t-6sin²t cos t+3sin t cos²t-4cos³ t=0; очевидно cos t≠0; tg t=p;
3p³-6p²+3p-4=0; домножаем на 9 и замена 3p=q: q³-6q+9q-36=0;
(q-2)³-3(q-2)-34=0;
но
Вот этот корень мы и искали. Подставлять найденное p для выписывания b, а затем x, сил уже не осталось.
Возможно, я где-то ошибся, но ошибку пока не вижу. Засим разрешите откланяться.
сутки состоят из целого числа часов,
часы состоят из целого числа минут,
минуты состоят из целого числа секунд.
Значит надо искать сомножители 715 - узнать вообще на сколько равных целых кусочков можно разделить это число:
715=5*11*13
получается, что возможны такие варианты:
715 минут - это
1) 5 суток по 11 часов, в каждом часе 13 минут
2) 5 суток по 13 часов, в каждом часе 11 минут
3) 11 суток по 5 часов, в каждом часе 13 минут
4) 11 суток по 13 часов, в каждом часе 5 минут
5) 13 суток по 5 часов, в каждом часе 11 минут
6)13 суток по 11 часов, в каждом часе 5 минут
по условию "минут в часе меньше, чем часов в сутках" - значит варианты 1, 3 и 5 не верны,
в оставшихся вариантах умножим часы на минуты - узнаем, сколько минут в сутках: на это число должно нацело делиться суточное к-во секунд - известные нам 1001:
5 суток по 13 часов, в каждом часе 11 минут - 143 минуты в сутках
11 суток по 13 часов, в каждом часе 5 минут - 65 минут в сутках
13 суток по 11 часов, в каждом часе 5 минут 55 минут в сутках
разложим на множители 1001
1001=7*11*13
вот они, знакомые 11*13 = 143
Получается, что только первый вариант имеет такие числа, чтобы суточное количество секунд нацело делилось на суточное к-во минут!
Итак, на планете Шелепука
неделя состоит из 5 суток,
сутки состоят из 13 часов,
час состоит из 11 минут,
минута состоит из 1001/143 = 7 секунд!
Ура!))
Угадываем корни 2 и - 2. Заметим, что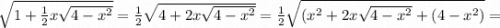
1) уравнение принимает вид
уравнение принимает вид
Исследуем знак второй производной: f''(x)=0 - когда где
где
2) уравнение принимает вид
уравнение принимает вид
На этом участке подобное рассуждение не проходит; кроме x=2 точно есть корень слева от нуля, поскольку f(0)>6. Будем рассуждать иначе.
Обе части положительны, смело возводим в квадрат (а можно было и к половинному углу свести):
6-6cos 2t-10sin 2t+2sin 2t cos 2t=0;
12sin² t-20 sin t cos t+4sin t cos t(cos² t-sin² t)=0; sin t=0 (⇒ a=0; b =2; x=2) или 3 sin t-5cos t+cos³ t-cos t sin² t=0;
(3sin t-5cos t)(cos²t+sin²t)+cos³ t-cos t sin^2 t=0;
3sin³t-6sin²t cos t+3sin t cos²t-4cos³ t=0; очевидно cos t≠0; tg t=p;
3p³-6p²+3p-4=0; домножаем на 9 и замена 3p=q: q³-6q+9q-36=0;
(q-2)³-3(q-2)-34=0;

Вот этот корень мы и искали. Подставлять найденное p для выписывания b, а затем x, сил уже не осталось.
Возможно, я где-то ошибся, но ошибку пока не вижу. Засим разрешите откланяться.