Перед вами случайная выборка из 25 - учеников 8 - го класса с данными об их росте: 166 165 163 166 168 170 165 165 165 165 164 168 165 164 161 166 166 167 164 163 168 167 167
Постройте по ней таблицу частот: и ответьте с её на вопросы:
1. В каком диапазоне изменялся рост учеников?
2.Какой рост встречался в выборке чаще всего?
Напишите ответ, и объясните как и почему. А то я понять совсем не могу, эту тему
84
Объяснение:
Воспользуемся формулой С из 9 по 3 : 9!/ (3! * 6! ) = 84
9! - если расположить все точки на коружности в 1 линию , то коллличество их перестановок будет равняться 9! или 1-ю точку мы можем выбрать 9-тью ую - 8-мью тью - 7-мью и так далее => 9 * 8 * 7 * ... * 1
Почему 9! надо делить на 6! ? - Так как , нам нужно выбрать только 3 точки для того чтобы получился треугольник => все перестановки , которые мы можем получить из оставшихся 6-ти точек нам не интересно => мы колличество перестоновок с 6-ю оставшимися точками исключаем
Почему 9! надо делить на 3! ? - Когда мы выбрали 3 точки , то нам не важен их порядок , то есть , пронумеруем выбранные точки : 1-ая точка , имеет номер 1 , 2-ая - 2 , 3-я - 3 , тода нам не важно в каком порядке они будут располагаться (123 или 321 или 312 и так далее) => мы исключаем кол-во перестановок с этими вершинами
1)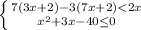
7(3x+2)-3(7x+2)<2x
21x+14-21x-6<2x
8<2x
-2x<-8
x>4
x²+3x-40≤0
x²+3x-40=(x-5)(x+8)
D=13²
x1=5
x2=-8
(x-5)(x+8)≤0
5 -8
x∈[-8;5]
После объединения в один чертёж:
ответ: x∈(4;5]
2)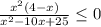
x²-10x+25≠0
D=0
x≠5
x²-10x+25=(x-5)²
x²(4-x)≤0
-x²(x-4)≤0
⇒ -x²(x-4)*(x-5)²≤0
-x²=0
x=0(знак на чертеже дублируется)
x-4=0
x=4
(x-5)²=0
x=5(знак дублируется и 5 выкалывается)
ответ: x∈[4;5)∪(5;∞)
3)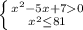
x²-5x+7>0
x²-5x+7
D=25-28=-3
⇒x>0 при любых x
Дополнительно: После D=-x - не всегда неравенство имеет решение - надо смотреть по графику (в вашем случаи - при любых x)
x²≤81
x²-81≤0
(x-9)(x+9)≤0
9;-9
ответ: x∈[-9;9]