добавим к обоим частям уравнений +1 +4 +9 и перегруппируем так, чтобы видеть квадраты двучленов
теперь выделяем квадраты
так как l, m, n целые числа, то целыми будут числа l-1,m+2,n-3 и их квадраты, при этом квадраты равны либо 0 либо 1 (квадраты целых чисел либо 0 либо натуральное число) потому что если хотя бы один из квадратов равен 4=2^2 или больше то л.ч.уравнения больше за правую и искомых троек чисел не существует
но так как из всех возможных 8 сумм из 0 и 1, только 1+1+1=3
то
откуда l-1=1 или l-1=-1
m+2=1 или m+2=-1
n-3=1 или n-3=-1
значит l=2 или l=0, m=-1 или m=-3, n=4 или n=2
итого восемь пар решений (l;m;n)
(2;-1;4)
(2;-1;2)
(0;-1-;4)
(0;-1;2)
(2;-3;4)
(2;-3;2)
(0;-3;4)
(0;-3;2)
вторая задача
обозначим учеников через 1,2,..8, а кружки через А,Б,В,Г,Д
не ограничивая общности если 1й ходит только в кружок А, то остальные в кружок А ходить не могут, иначе сразу противоречие (если например второй ходит в кружок А и другой кружок, например Б, то он ходит во все кружки в которые ходит 1, что невозможно)
т.е. ученики ходят минимум в 2 кружка (могут и в большее).
никто из ребят не может ходить сразу во все пять кружков, иначе он будет ходить во все кружки которые ходит любой другой из ребят
Далее если например 1й ученик ходит в 4 кружка (например А,Б,В,Г), то
никто не может ходить в комбинацию двух или трех кружков из кружков А,Б,В, Г так как 1й будет ходить во все кружки что и второй
остаются возможными варианты Б,Е или В,Е, или Г,Е или А,Е или А,Б,Е, или Б, В, Е, или В,Г, Е, или А,Г,Е или Б, В, Г, Е или А, Б, В, Е, или А,Г, В, Е или А, Б, Г, Е
если 2й ходит в 2 кружка из оставшихся например Б,Е , то исключая противоречивые согласно условию остаются возможными 6 вариантов или В,Е, или Г,Е или А,Е или В,Г, Е, или А,Г,Е или А,Г, В, Е (среди которых есть противоречивые например В,Е и А,Г, В, Е) и вариантов получается меньше чем 6, и для какогото из учеников не остается варианта выбора
если 2й ходит в 3 кружка, например А,Б,Е, то исключая остаются возможности для других учеников или В,Е, или Г,Е или В,Г, Е, или А,Г,Е или Б, В, Г, Е или А,Г, В, Е - 6 возможностей , среди которых есть противоречивые (например Г,Е и А,Г, В, Е) и возможностей получается меньше чем оставшихся учеников.
если 2й ходит в 4 кружка например Б, В, Г, Е, то исключая согласно условию остаются возможности или А,Б,Е или А,Г,Е или А, Б, В, Е, или А,Г, В, Е или А, Б, Г, Е - 5 возможностей - меньше чем оставшихся учеников. Следовательно и такой вариант событий не подходит.
Таким образом получаем что не один ученик не может ходить в четыре кружка.
Обьединяя получаем искомое, что согласно правилам и условию каждый школьник занимается в 2х или 3х кружках.
1.Найдите область определения функции:
а) y=3/(х+7) , знаминатель не равен нулю: х+7≠0 х≠-7
E(y)∈(-∞;-7)U(-7;+∞)
б) F(x)=√(3-х) ,подкоренное выражение ≥0 : 3-х≥0 x≤3
E(x)∈(-∞;3]
2.Найдите нули функции-
а) у=3х+1
при x=0 : у=3*(0)+1 y=1
при y=0 : 0=3x+1 x=-1/3
y0=(-1/3;0)
ответ: x0=(0;1) , y0=(-1/3;0)
б) у=х^2 -9
x0=-b/2a=0/-2=0
y0=(0)^2 -9=-9
ответ:x0=0 , y0=-9
3. При каких значениях t функция у=2t -1 принимает отрицательные значения?
2t -1<0
2t<1
t<0,5
t∈(-∞;0,5)
ответ:y<0 ,при t∈(-∞;0,5).
добавим к обоим частям уравнений +1 +4 +9 и перегруппируем так, чтобы видеть квадраты двучленов
теперь выделяем квадраты
так как l, m, n целые числа, то целыми будут числа l-1,m+2,n-3 и их квадраты, при этом квадраты равны либо 0 либо 1 (квадраты целых чисел либо 0 либо натуральное число) потому что если хотя бы один из квадратов равен 4=2^2 или больше то л.ч.уравнения больше за правую и искомых троек чисел не существует
но так как из всех возможных 8 сумм из 0 и 1, только 1+1+1=3
то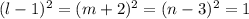
откуда l-1=1 или l-1=-1
m+2=1 или m+2=-1
n-3=1 или n-3=-1
значит l=2 или l=0, m=-1 или m=-3, n=4 или n=2
итого восемь пар решений (l;m;n)
(2;-1;4)
(2;-1;2)
(0;-1-;4)
(0;-1;2)
(2;-3;4)
(2;-3;2)
(0;-3;4)
(0;-3;2)
вторая задача
обозначим учеников через 1,2,..8, а кружки через А,Б,В,Г,Д
не ограничивая общности если 1й ходит только в кружок А, то остальные в кружок А ходить не могут, иначе сразу противоречие (если например второй ходит в кружок А и другой кружок, например Б, то он ходит во все кружки в которые ходит 1, что невозможно)
т.е. ученики ходят минимум в 2 кружка (могут и в большее).
никто из ребят не может ходить сразу во все пять кружков, иначе он будет ходить во все кружки которые ходит любой другой из ребят
Далее если например 1й ученик ходит в 4 кружка (например А,Б,В,Г), то
никто не может ходить в комбинацию двух или трех кружков из кружков А,Б,В, Г так как 1й будет ходить во все кружки что и второй
остаются возможными варианты Б,Е или В,Е, или Г,Е или А,Е или А,Б,Е, или Б, В, Е, или В,Г, Е, или А,Г,Е или Б, В, Г, Е или А, Б, В, Е, или А,Г, В, Е или А, Б, Г, Е
если 2й ходит в 2 кружка из оставшихся например Б,Е , то исключая противоречивые согласно условию остаются возможными 6 вариантов или В,Е, или Г,Е или А,Е или В,Г, Е, или А,Г,Е или А,Г, В, Е (среди которых есть противоречивые например В,Е и А,Г, В, Е) и вариантов получается меньше чем 6, и для какогото из учеников не остается варианта выбора
если 2й ходит в 3 кружка, например А,Б,Е, то исключая остаются возможности для других учеников или В,Е, или Г,Е или В,Г, Е, или А,Г,Е или Б, В, Г, Е или А,Г, В, Е - 6 возможностей , среди которых есть противоречивые (например Г,Е и А,Г, В, Е) и возможностей получается меньше чем оставшихся учеников.
если 2й ходит в 4 кружка например Б, В, Г, Е, то исключая согласно условию остаются возможности или А,Б,Е или А,Г,Е или А, Б, В, Е, или А,Г, В, Е или А, Б, Г, Е - 5 возможностей - меньше чем оставшихся учеников. Следовательно и такой вариант событий не подходит.
Таким образом получаем что не один ученик не может ходить в четыре кружка.
Обьединяя получаем искомое, что согласно правилам и условию каждый школьник занимается в 2х или 3х кружках.
такое возможно
например
1 - А,Б, 2 - Б,В, 3 - В,Г, 4 - Г,Д, 5 -Д,Е 6 - А,Е, 7 - Б,Е 8 - Г,Е