Первый член последовательности а1=13, а каждый следующий на 5 меньше предыдущего. Найдите шестой член данной последовательности. В ответе укажите только число без пробелов. Если получится отрицательное число, то пробела между знаком и числом не ставить.

Показать ответ

Ответ:

IiiPON4IKiiI

03.12.2020 11:59

1) При x ≥ 9 значения функции y = -5x - 3 не больше -48.

2) При x > -4 значения функции y = -3/4 *x - 1 меньше 2.

Объяснение:

Рисунки прилагаются.

1) y = -5x - 3 линейная функция, график прямая линия, пересекает ось OY в точке (0; --3).

Выберем еще одну точку и построим график функции: x = 10; y = -50-3 = -53.

При каких значениях x значения функции не больше (значит меньше или равно) -48?

Построим в этой же системе координат прямую y = -48.

По графикам видно, что что -5x - 3 ≤ -48 при x ≥ 9

Проверим аналитически:

-5x -3 ≤ -48; -5x ≤ -48 +3; -5x ≤ -45; x ≥ 9.

2) y = -3/4*x - 3 = -0,75x - 1 линейная функция, график прямая линия, пересекает ось OY в точке (0; -1).

Выберем еще одну точку и построим график функции: x = 4;

y = -0,75*4 -1 = -3 - 1 = -4.

При каких значениях x значения функции меньше 2?

Построим в этой же системе координат прямую y = 2.

По графикам видно, что -0,75x - 1 ≤ -2 при x > -4

Проверим аналитически:

-0,75x -1 < 2; -0,75x < 3; x > -4.

1) постройте график функции у=-5х-3 и найдите при каких значениях у не больше -48 2) постройте графи

0,0(0 оценок)

Ответ:

leonidbobnev

04.10.2021 20:45

Смотри решение.

Объяснение:

решения (через дискриминант):

$x^2+5x+6=0\\a=1; b=5; c=6\\D=b^2-4ac\\D=5^2-4*1*6\\D=25-24\\D=1\\\sqrt{D}=\sqrt{1}=1\\x_{1}=\frac{-b+\sqrt{D}}{2a}=\frac{-5+1}{2}=\frac{-4}{2}=-\frac{4}{2}=-2\\x_{2}=\frac{-b-\sqrt{D}}{2a}=\frac{-5-1}{2}=\frac{-6}{2}=-\frac{6}{2}=-3\\$

Порядок решения:

а. Записываем уравнение в исходном виде;

б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);

в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.

решения (через теорему Виетта):

Сумма 2 корней уравнения равняется коэффициенту b, взятому с противоположным знаком.

Произведение 2 корней уравнения равняется свободному коэффициенту в данном уравнении.

Общая формула квадратного уравнения: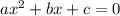 $ax^2+bx+c=0\\$ (для справок).