Пирожные в кафе «мечта» стоят x руб., а такие же пирожные в кафе «весна» — y руб. определите границы, во сколько раз дешевле пирожные стоят в кафе «мечта», чем в кафе «весна», если 35
силий Тёркин»? Назовите подзаголовок поэмы. 3. Почему поэт пишет, что «на войне сюжета нету» и что книга «без начала и конца»? 4. Во для анализа главы «Переправа»: а) На какие части разделяют главу слова «Переправа, переправа...»? Каким настроением проникнута каждая часть главы? С какой интонацией следует читать эти строки? б) Что является «лейтмотивом» данной главы? Почему? в) Каким в этой главе предстаёт перед читателем Василий Тёркин? 5. Во для анализа главы «О награде»: а) Как построена эта глава? Дайте характеристику частей этой главы? б) Как проявляется здесь стилевое многообразие поэмы? в) Что нового об образе Тёркина мы узнаём в этой главе? г) Можем ли сказать, что автор сроднился с Тёркиным? В чём это проявляется? Что значит слово «родина» для каждого из них? е) Выделите в главе строки, которые являются рефреном произведения. Как вы думаете, почему именно такой рефрен включён Твардо
2) число -20 - отрицательное, оно больше числа 5,7. Так что будем отнимать от -20 5,7. -20 - 5,7 = - 14,3. ответ в этом примере получится отрицательный, так как -20 больше
4) Для того, чтобы поделить десятичные дроби, нужно перенести все запятые вправо так, чтобы мы делили на целое число. В данном случае, мы будем делить 187,5 на 75. 187 делить на 75 = 2 (целая часть). После целой части мы ставим запятую и делим 375 (остаток от деления) на 75. И получаем 5. ответ: 2,5
6) Складываем целые части дробей с целыми, а десятичные с десятичными. 54 + 5, А 7 + 63. Не забываем добавлять остатки от десятичных частей к целым. Получаем 60,33
8)Самое обыкновенное умножение. Можно решать столбиком. Каждое число друг под другом. Умножаем все числа друг на друга. Получаем 21,14
10) Переводим смешанную дробь 1 в неправильную. (1 * 14) + 5 = . Домножаем первую дробь на 2, чтобы получить общий знаменатель 14. Теперь решаем = . Умножаем на 12,6. Для удобства переведем 12,6 в неправильную дробь . Числитель умножаем на числитель, а знаменатель на знаменатель. Получим . Делим числитель на знаменатель и получаем 22,5
12) Переводим смешанные дроби в скобках в неправильные. Получим и . Приводим их к общему знаменателю, равному 90. Для этого домножаем первую дробь на 10, а вторую на 9. Получим и . Отнимаем дроби друг от друга. Для этого отнимаем числитель 320 - 198. Получаем 122. : . Чтобы поделить первую дробь на вторую, вторую дробь нужно перевернуть. Получим * 90. Сокращаем 90, получаем 122.
14) Чтобы не пришлось возводить оба больших числа в квадрат, вынесем степень за скобку . Получаем . 152 умножаем на 152, получаем 23104. 23104 делим на 100, то есть переносим запятую на 2 числа (число нолей в 100) влево. Получаем 231,04
16) Переведем смешанную дробь 6 в неправильную = . Делим дроби друг на друга. Для этого перевернем вторую дробь. * .
Сокращаем 13. 82 делим на 2. Получаем 41.
18) Сократим 24,2 и 0,242. Поделим числа друг на друга. Получим 100.
Сократим 35,6 и 3,56. Получим 10. 10 * 100 = 1000
20) Умножим на каждое число в скобках. Получим . . Вынесем числа из под корня. Получаем 10 + 5 = 15
22) Возводим в квадрат. = 16 = 7. 16 * 7 = 112. 112 делим на 16, получаем 7
силий Тёркин»? Назовите подзаголовок поэмы. 3. Почему поэт пишет, что «на войне сюжета нету» и что книга «без начала и конца»? 4. Во для анализа главы «Переправа»: а) На какие части разделяют главу слова «Переправа, переправа...»? Каким настроением проникнута каждая часть главы? С какой интонацией следует читать эти строки? б) Что является «лейтмотивом» данной главы? Почему? в) Каким в этой главе предстаёт перед читателем Василий Тёркин? 5. Во для анализа главы «О награде»: а) Как построена эта глава? Дайте характеристику частей этой главы? б) Как проявляется здесь стилевое многообразие поэмы? в) Что нового об образе Тёркина мы узнаём в этой главе? г) Можем ли сказать, что автор сроднился с Тёркиным? В чём это проявляется? Что значит слово «родина» для каждого из них? е) Выделите в главе строки, которые являются рефреном произведения. Как вы думаете, почему именно такой рефрен включён Твардо
Объяснение:
2) - 14,3
4) 2,5
6) 60,33
8) 21,14
10) 22,5
12) 122
14) 231,04
16) 41
18) 1000
20) 15
22) 7
Объяснение:
2) число -20 - отрицательное, оно больше числа 5,7. Так что будем отнимать от -20 5,7. -20 - 5,7 = - 14,3. ответ в этом примере получится отрицательный, так как -20 больше
4) Для того, чтобы поделить десятичные дроби, нужно перенести все запятые вправо так, чтобы мы делили на целое число. В данном случае, мы будем делить 187,5 на 75. 187 делить на 75 = 2 (целая часть). После целой части мы ставим запятую и делим 375 (остаток от деления) на 75. И получаем 5. ответ: 2,5
6) Складываем целые части дробей с целыми, а десятичные с десятичными. 54 + 5, А 7 + 63. Не забываем добавлять остатки от десятичных частей к целым. Получаем 60,33
8)Самое обыкновенное умножение. Можно решать столбиком. Каждое число друг под другом. Умножаем все числа друг на друга. Получаем 21,14
10) Переводим смешанную дробь 1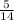 в неправильную. (1 * 14) + 5 =
в неправильную. (1 * 14) + 5 = 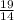 . Домножаем первую дробь на 2, чтобы получить общий знаменатель 14. Теперь решаем
. Домножаем первую дробь на 2, чтобы получить общий знаменатель 14. Теперь решаем  =
= 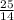 . Умножаем на 12,6. Для удобства переведем 12,6 в неправильную дробь
. Умножаем на 12,6. Для удобства переведем 12,6 в неправильную дробь 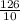 . Числитель умножаем на числитель, а знаменатель на знаменатель. Получим
. Числитель умножаем на числитель, а знаменатель на знаменатель. Получим 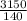 . Делим числитель на знаменатель и получаем 22,5
. Делим числитель на знаменатель и получаем 22,5
12) Переводим смешанные дроби в скобках в неправильные. Получим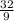 и
и 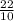 . Приводим их к общему знаменателю, равному 90. Для этого домножаем первую дробь на 10, а вторую на 9. Получим
. Приводим их к общему знаменателю, равному 90. Для этого домножаем первую дробь на 10, а вторую на 9. Получим 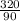 и
и 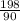 . Отнимаем дроби друг от друга. Для этого отнимаем числитель 320 - 198. Получаем 122.
. Отнимаем дроби друг от друга. Для этого отнимаем числитель 320 - 198. Получаем 122. 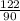 :
: 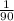 . Чтобы поделить первую дробь на вторую, вторую дробь нужно перевернуть. Получим
. Чтобы поделить первую дробь на вторую, вторую дробь нужно перевернуть. Получим 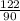 * 90. Сокращаем 90, получаем 122.
* 90. Сокращаем 90, получаем 122.
14) Чтобы не пришлось возводить оба больших числа в квадрат, вынесем степень за скобку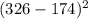 . Получаем
. Получаем 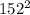 . 152 умножаем на 152, получаем 23104. 23104 делим на 100, то есть переносим запятую на 2 числа (число нолей в 100) влево. Получаем 231,04
. 152 умножаем на 152, получаем 23104. 23104 делим на 100, то есть переносим запятую на 2 числа (число нолей в 100) влево. Получаем 231,04
16) Переведем смешанную дробь 6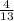 в неправильную =
в неправильную = 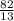 . Делим дроби друг на друга. Для этого перевернем вторую дробь.
. Делим дроби друг на друга. Для этого перевернем вторую дробь. 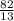 *
* 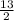 .
.
Сокращаем 13. 82 делим на 2. Получаем 41.
18) Сократим 24,2 и 0,242. Поделим числа друг на друга. Получим 100.
Сократим 35,6 и 3,56. Получим 10. 10 * 100 = 1000
20) Умножим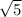 на каждое число в скобках. Получим
на каждое число в скобках. Получим 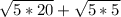 .
. 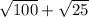 . Вынесем числа из под корня. Получаем 10 + 5 = 15
. Вынесем числа из под корня. Получаем 10 + 5 = 15
22) Возводим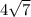 в квадрат.
в квадрат. 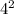 = 16
= 16 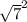 = 7. 16 * 7 = 112. 112 делим на 16, получаем 7
= 7. 16 * 7 = 112. 112 делим на 16, получаем 7