ПЛ


1.Применение ……. позволяет у преобразования
выражений.
2. Куб разности двух выражений равен кубу первого
выражения минус ……. на второй плюс утроенное
произведение первого выражения на квадрат второго минус
куб второго выражения”.
3. Для упрощения данного выражения (4 – 5а) 2 – 6а(3а + 1) +
+(7а–2)(2 + 7а). воспользуемся формулами квадрата разности
и разности квадратов, …., а затем приведем…...
4. Чтобы найти разность дробных выражений с разными
знаменателями, нужно……., а затем найти их разность как
разность дробных выражений с одинаковыми знаменателями:
5. Равенство, верное при всех допустимых значениях переменных
называют …….
6. Замену одного выражения другим, ……….ему, называют
тождественным преобразованием.
7. Выражения , составленные из…….. сложения, вычитания,
умножения и возведения в степень называют целыми
выражениями.
8. При изменении знака дроби нужно …………… этой дроби.
9. Чтобы………, нужно перемножить отдельно их числители и
знаменатели и первое произведение записать числителем, а
второе – знаменателем.
10. Чтобы разделить одно дробное выражение на другое, нужно
делимое умножить на дробь, …….

Все стороны квадрата равны. Допустим сторона квадра будет x.

Тогда площадь квадрата будет равна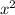 . По условию площадь увеличилась в 16 раз, то есть стала равна 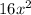. Так как она увеличилась, следовательно увеличили саму сторону квадрата. Увеличили ее в 4 раза, так как новая площадь это 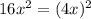. Мы узнали, что сторона квадрата увеличилась в 4 раза, теперь узнаем во сколько раз увеличится периметр. Так как периметр квадрата без увеличение его сторон будет равен 4x, то при увеличении стороны в 4 раза он будет равен 4*4x=16x. То есть периметр увеличился в 4 раза.

В решении.

Объяснение:

Решить неравенство:

1) 3(х + 4) + 2(3х - 2) > 5х - 3(2х + 4)

Раскрыть скобки:

3х+12+6х-4 > 5х-6х-12

Привести подобные члены:

9х+х >  -12-8

10х > -20

х > -20/10

х > -2

x∈(-2; +∞)     ответ а)

Неравенство строгое, скобки круглые.

2) 2х - 6 - 5(2 - х) <= 12 - 5(1 - x)

Раскрыть скобки:

2х-6-10+5х <= 12-5+5х

Привести подобные члены:

7х-5х <= 7+16

2х <= 23

x <= 23/2

x <= 11,5

х∈(-∞; 11,5]      ответ б)

Неравенство нестрогое, скобка квадратная, а знаки бесконечности всегда с круглыми скобками.

3) х + 2 < 5(2х + 8) + 13(4 - х) - 3(х - 2)

Раскрыть скобки:

х+2 < 10х+40+52-13х-3х+6

Привести подобные члены:

х+6х < 98-2

7х < 96

х < 96/7

x < 13 и 5/7

х∈(-∞; 13 и 5/7)     ответ в)

Неравенство строгое, скобки круглые.