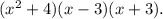Объяснение:
В каком виде представлены выражения, в таком виде и будем решать:
(4ас^2)^3 •(0,5а^3 •с)^2=(2^2)^3 •(1/2)^2 •а^(3+3•2) •с^(2•3+2)=2^(2•3-2) •а^9 •с^8=2^4 •а^9 •с^8=16а^9 •с^8
(2/(3х^2 •у^3))^3 •(-9х^4)^2=8/3^3 •(-(3^2))^2 •х^(-2•3+4•2) •у^(-3•3)=8•3^(-3+2•2) •х^(-6+8) •у^(-9)=(8•3)/(х^2 •у^9)=24/(х^2 •у^9)
-(-х^2 •у^4)^4 •(6х^4 •у)^2=-36х^(2•4+4•2) •у^(4•4+2)=-36х^(8+8) •у^18=-36х^16 •у^18
(-10а^3 •b^2)^5 •(-0,2ab^2)^5=(-10)^5 •(-2/10)^5 •a^(3•5+5) •b^(2•5+2•5)=32•10^(5-5) •a^20 •b^(10+10)=32a^20 •b^20
Для того чтобы разложить на множители выражение вида , где — числа, достаточно решить квадратное уравнение , где , и применить формулу разложения: где и — корни данного квадратного уравнения, после чего нужно сделать обратную замену.
Итак, имеем биквадратный трехчлен . Сделаем подходящую замену: Получили квадратный трехчлен .
Решим уравнение при теоремы Виета:
Получили корни:
Подставим полученные корни в формулу: Сделаем обратную замену: Применим формулу разности квадратов и получаем окончательное разложение данного биквадратного трехчлена:
Воспользуемся методом группирования (группировки):
ответ:
Объяснение:
В каком виде представлены выражения, в таком виде и будем решать:
(4ас^2)^3 •(0,5а^3 •с)^2=(2^2)^3 •(1/2)^2 •а^(3+3•2) •с^(2•3+2)=2^(2•3-2) •а^9 •с^8=2^4 •а^9 •с^8=16а^9 •с^8
(2/(3х^2 •у^3))^3 •(-9х^4)^2=8/3^3 •(-(3^2))^2 •х^(-2•3+4•2) •у^(-3•3)=8•3^(-3+2•2) •х^(-6+8) •у^(-9)=(8•3)/(х^2 •у^9)=24/(х^2 •у^9)
-(-х^2 •у^4)^4 •(6х^4 •у)^2=-36х^(2•4+4•2) •у^(4•4+2)=-36х^(8+8) •у^18=-36х^16 •у^18
(-10а^3 •b^2)^5 •(-0,2ab^2)^5=(-10)^5 •(-2/10)^5 •a^(3•5+5) •b^(2•5+2•5)=32•10^(5-5) •a^20 •b^(10+10)=32a^20 •b^20
Для того чтобы разложить на множители выражение вида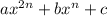 , где
, где 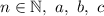 — числа, достаточно решить квадратное уравнение
— числа, достаточно решить квадратное уравнение 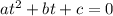 , где
, где 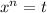 , и применить формулу разложения:
, и применить формулу разложения: 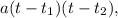 где
где 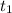 и
и 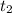 — корни данного квадратного уравнения, после чего нужно сделать обратную замену.
— корни данного квадратного уравнения, после чего нужно сделать обратную замену.
Итак, имеем биквадратный трехчлен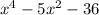 . Сделаем подходящую замену:
. Сделаем подходящую замену: 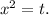 Получили квадратный трехчлен
Получили квадратный трехчлен 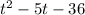 .
.
Решим уравнение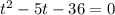 при теоремы Виета:
при теоремы Виета:
Получили корни: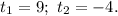
Подставим полученные корни в формулу: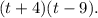 Сделаем обратную замену:
Сделаем обратную замену: 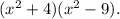 Применим формулу разности квадратов
Применим формулу разности квадратов 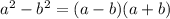 и получаем окончательное разложение данного биквадратного трехчлена:
и получаем окончательное разложение данного биквадратного трехчлена: 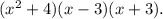
Воспользуемся методом группирования (группировки):
ответ: