Площади фигуры, ограниченной графиком функции, содержащей квадратный корень Вычислить площадь фигуры, ограниченной линиями:
y=корень из(x+3), x=10,y=0

Показать ответ

Ответ:

2303010

28.04.2022 23:01

X⁷(x-1) -5x⁵(x - 1) - 2x⁴(x - 1) + 7x³(x - 1) + 4x²(x - 1) - 3x(x - 1) - 2(x - 1) =
=(x-1)(x⁷ - 5x⁵ - 2x⁴ + 7x³ + 4x² - 3x - 2) =
=(x-1)(x⁶(x-1) +x⁵(x-1) - 4x⁴(x-1) - 6x³(x-1) + x²(x-1) + 5x(x-1) + 2(x-1)) =
=(x-1)(x-1)(x⁶ + x⁵ - 4x⁴ - 6x³ + x² + 5x + 2) =
=(x-1)(x-1)(x⁵(x-1) +2x⁴(x-1) - 2x³(x-1) - 8x²(x-1) - 7x(x-1) -2(x-1)) =
=(x-1)³(x⁵ + 2x⁴ - 2x³ - 8x² - 7x - 2) =
=(x-1)³(x⁴(x-2) + 4x³(x-2) + 6x²(x-2) + 4x(x-2) + (x-2)) =
=(x-1)³(x-2)(x⁴ + 4x³ + 6x² + 4x + 1) = (x-1)³(x-2)(x+1)⁴

ответ: (x-1)³(x+1)⁴(x-2)

0,0(0 оценок)

Ответ:

ирка137

10.05.2021 12:01

За интеграл я буду Июиспользовать вот этот знак:

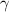
$\gamma$

4 пример:

1) Перепишите дробь:

$\gamma - \frac{1}{x} + \frac{2}{x + 6} dx$

2) Использовать свойства интегралов:

$- \gamma \frac{1}{x} dx + \gamma \frac{2}{x + 6} dx$

3) Вычислить интегралы и прибавить константу интегрирования С:

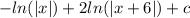
- ln( |x| ) + 2 ln( |x + 6| ) + c

5 пример:

1) Найти неопределённый интеграл:

$\gamma x \sqrt{x + 8} dx$

2) Упростить интеграл, используя метод замены переменной:

$\gamma t \sqrt{t} - 8 \sqrt{t} dt$

3) Преобразовать выражения:

$\gamma t \times {t}^{ \frac{1}{2} } - 8 {t}^{ \frac{1}{2} } dt$

4) Вычислить произведение:

$\gamma {t}^{ \frac{3}{2} } - 8 {t}^{ \frac{1}{2} } dt$

5) Использовать свойство интегралов:

$\gamma {t}^{ \frac{3}{2} } dt - \gamma 8 {t}^{ \frac{1}{2} } dt$

6) Вычислить интегралы:

$\frac{2 {t}^{2} \sqrt{t} }{5} - \frac{16t \sqrt{t} }{3}$

7) Выполнить обратную замену:

$\frac{2 {(x + 8)}^{2} \times \sqrt{x + 8} }{5} - \frac{16(x + 8) \sqrt{x + 8} }{3}$

8) Упростить выражение:

$\frac{2 \sqrt{x + 8} \times ( {x}^{2} + 16x + 64) }{5} - \frac{16(x + 8) \sqrt{x + 8} }{3}$

9) Вернуть пределы интегрирования и подставить в пример (8):

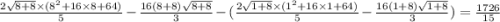
$\frac{2 \sqrt{8 + 8} \times ( {8}^{2} + 16 \times 8 + 64) }{5} - \frac{16(8 + 8) \sqrt{8 + 8} }{3} - ( \frac{2 \sqrt{1 + 8} \times ( {1}^{2} + 16 \times 1 + 64)}{5} - \frac{16(1 + 8) \sqrt{1 + 8} }{3} ) = \frac{1726}{15}$

6 пример