Плотность свинца равна 11,4 г/см^311,4г/см
3
. Найдите массу свинцовой плиты, длина которой 1,81,8 м, ширина 5\cdot10^{-1}5⋅10
−1
м и толщина 1,5\cdot10^{-1}1,5⋅10
−1
м.
Решение: 11,4 г/см^3 = 11,4 т/м^311,4г/см
3
=11,4т/м
3
, так как 1 г= 10^{-6}1г=10
−6
т, 1 см^{3}=10^{-6} м^31см
3
=10
−6
м
3
.
1) y-2. ОДЗ: y≠2
2) a-1. ОДЗ: a≠1
Объяснение:
№1. (y+2+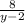 ):
):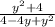 =
=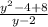 :
: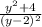 =
=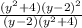 =y-2. ОДЗ: y≠2
=y-2. ОДЗ: y≠2
№2. (a+1+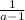 ):
):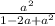 =
=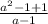 :
: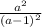 =
=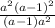 =a-1. ОДЗ: a≠1
=a-1. ОДЗ: a≠1
ОДЗ - область допустимых значений. Т.е. когда мы сокращаем что-либо в числителе и знаменателе, то мы можем потом включить это число в решения. То есть, например, в первом номере мы сокращаем скобку y-2. Тем самым мы сознательно "пропускаем" в решения (если бы мы не просто упрощали, а решали такое уравнение). Но эта скобка стоит у нас в знаменателе. А знаменатель не может быть равен 0, т.к. на 0 делить нельзя. Значит нужно исключить решение такого уравнения: y-2=0, т.е. y не равен 2. В первом номере скобку y^2+4 мы не выносим в ОДЗ, потому что если мы будем решать такое уравнение: y^2+4=0, то увидим, что оно никогда не будет равно 0. Квадрат любого числа - число неотрицательное по определению, а неотрицательное+положительное=положительное, т.е. не равное 0. Поэтому эту скобку мы не вносим в ОДЗ. Во втором номере мы сокращаем a^2, т.е. автоматически "пропускаем" a=0. Значит нужно его исключить. Также мы сокращаем скобку a-1, значит нужно исключить решение уравнения a-1=0, т.е. a не равно 1.
решается по формуле d=b²-4ac
a b c
3x²+x-30=0
D=1²-4·3· (-30)=1+360=361 , D больше 0 значит имеет 2 корня
x 1=-b+√D÷(2a) x2=-b-√D÷(2a)
∧ 2a в знаменатель ∧ 2a в знаменатель
x1= -1+√361÷(2·3) x2=-1-√361÷(2·3)
x1=-1+19 ÷6 x2= -1-19÷6
x1=18÷6 x2=-20÷6 ( сокращаем -20 и 6 )
x1=3 x2=-10÷3
ответ : x1=3 ; x2=-10÷3