приведем оба уравнения системы к виду y=kx+b(уравнение прямой).
Если две прямые и заданы уравнениями и , то на плоскости они могут быть:
1) и - прямые параллельны, следовательно они не пересекаются и, следовательно, система из таких прямых не имеет решений.
2) и - прямые совпадают, следовательно, система из таких прямых будет иметь бесконечное множество решений.
3) - прямые пересекаются в одной точке, следовательно, система из таких прямых будет иметь только одно решение.
Применим это для решения данной задачи:
Значит, при a=0 данная система не имеет решений.
Значит, при a=3 данная система имеет бесконечное множество решений.
При остальных значениях a система будет иметь только одно решение:
В итоге:
система имеет одно решение.
ответ: a=0 => система не имеет решений(x∈∅)
a=3 => система имеет бесконечное множество решений(x∈R)
a∈(-∞;0)∪(0;3)∪(3;+∞) => система имеет одно решение.
Дано: F(x)=x²+4 - функция, Хо = 1.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 2*x
Вычисляем в точке Хо = 1.
F'(1) = 2 - производная и F(1) = 5 - функция.
Записываем уравнения прямой.
Y = 2*(x - 1) + (5) = 2*x + 3 - касательная - ОТВЕТ
Рисунок к задаче в приложении.
2) Дано: F(x)=2*x²+ x - функция, Хо = 2.
F'(x) = 4*x + 1.
Вычисляем в точке Хо = 2.
F'(2) = 9 - производная и F(2) = 10 - функция.
Y = 9*(x - 2) + (10) = 9*x -8 - касательная - ОТВЕТ
3) Дано: F(x)=3*x² -6*x +1 - функция, Хо = 0.
F'(x) = 6*x -6.
Вычисляем в точке Хо = 0.
F'(0) = -6 - производная и F(0) = 1 - функция.
Y = -6*(x - 0) + (1) = -6*x + 1 - касательная - ОТВЕТ
Подробнее - на -
приведем оба уравнения системы к виду y=kx+b(уравнение прямой).
Если две прямые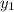
и 
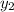заданы уравнениям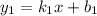и 
и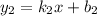 
, то на плоскости они могут быть:
1)
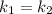и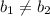 
- прямые параллельны, следовательно они не пересекаются и, следовательно, система из таких прямых не имеет решений.
2)
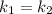и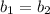 
- прямые совпадают, следовательно, система из таких прямых будет иметь бесконечное множество решений.
3)
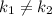- прямые пересекаются в одной точке, следовательно, система из таких прямых будет иметь только одно решение.
Применим это для решения данной задачи:
Значит, при a=0 данная система не имеет решений.
Значит, при a=3 данная система имеет бесконечное множество решений.
При остальных значениях a система будет иметь только одно решение:
В итоге:
ответ: a=0 => система не имеет решений(x∈∅)
a=3 => система имеет бесконечное множество решений(x∈R)
a∈(-∞;0)∪(0;3)∪(3;+∞) => система имеет одно решение.
Дано: F(x)=x²+4 - функция, Хо = 1.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 2*x
Вычисляем в точке Хо = 1.
F'(1) = 2 - производная и F(1) = 5 - функция.
Записываем уравнения прямой.
Y = 2*(x - 1) + (5) = 2*x + 3 - касательная - ОТВЕТ
Рисунок к задаче в приложении.
2) Дано: F(x)=2*x²+ x - функция, Хо = 2.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 4*x + 1.
Вычисляем в точке Хо = 2.
F'(2) = 9 - производная и F(2) = 10 - функция.
Записываем уравнения прямой.
Y = 9*(x - 2) + (10) = 9*x -8 - касательная - ОТВЕТ
3) Дано: F(x)=3*x² -6*x +1 - функция, Хо = 0.
Y = F'(Xo)*(x - Xo) + F(Xo) .
Находим первую производную - k - наклон касательной.
F'(x) = 6*x -6.
Вычисляем в точке Хо = 0.
F'(0) = -6 - производная и F(0) = 1 - функция.
Записываем уравнения прямой.
Y = -6*(x - 0) + (1) = -6*x + 1 - касательная - ОТВЕТ
Рисунок к задаче в приложении.
Подробнее - на -