Решение подобного биквадратного уравнения сводится к замене вида:
Исходя из области определения корнями будут:
ответ:
Область определения уравнения:
Преобразовывая область определения отбросим левую часть,так как корень равен неотрицательному числу(в данном случае числом является x,и при отрицательных x равенство не имеет место)
Возведем обе неотрицательные части в четвертую степень:
Решение подобного биквадратного уравнения сводится к замене вида:
1)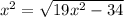
Область определения уравнения:
Возведем обе неотрицательные части в квадрат:
Решение подобного биквадратного уравнения сводится к замене вида: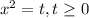
Исходя из области определения корнями будут:
ответ: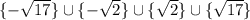
Область определения уравнения:
Преобразовывая область определения отбросим левую часть,так как корень равен неотрицательному числу(в данном случае числом является x,и при отрицательных x равенство не имеет место)
Возведем обе неотрицательные части в четвертую степень:
Решение подобного биквадратного уравнения сводится к замене вида: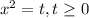
Исходя из области определения корнями будут:
ответ: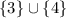
решается легко:
сначала нужно узнать, сколько кг винограда было у Незнайки.
для этого "обзываем" первоначальное кол-во винограда буквой n.
потом говорится, что он отдал первому другу половину винограда.
т.е. кол-во винограда n делим на 2. Получаем n/2.
потом он отдал половину от полученного кол-ва 2-ому другу.
т.е. полученное кол-во винограда (n/2) делим ещё на 2. Получаем n/4
потом он отдал половину от полученного кол-ва 3-ему другу.
т.е. полученное кол-во винограда (n/4) делим ещё на 2. Получаем n/8
потом он отдал половину от полученного кол-ва 4-ому другу.
т.е. полученное кол-во винограда (n/8) делим ещё на 2. Получаем n/16
получается такое выражение:
n/16=2 (кол-во винограда делим ноа кол-во, которое он отдал друзьям, получаем 2 кг)
n=2*16=32 кг (было у Незнайки сразу после сбора)
32-2=30 кг (от начального кол-ва винограда отнимаем конечное и получаем кол-во, раздаренное друзьям)
ответ:30 кг