Весь путь обозначим за 1(единицу) пусть х км/ч скорость первого автомобиля, значит время пути 1/х часов. тогда второй автомобиль первую половину пути проедет за 1/2*(х+15), а вторую половину пути за 1/2*50, где (х+15 )км/ч и 50 км/ч скорость второго автомобиля
1/2*(х+15) +1/2*50 =1/х
100+2(х+15) 1 = избавимся от знаменателей 2*(х+15)*100 х
Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила часов и против течения реки, на расстояние в 14 км, лодки затратила часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это часов. Составим уравнение:
x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.
пусть х км/ч скорость первого автомобиля, значит время пути 1/х часов.
тогда второй автомобиль первую половину пути проедет за 1/2*(х+15),
а вторую половину пути за 1/2*50, где (х+15 )км/ч и 50 км/ч скорость второго автомобиля
1/2*(х+15) +1/2*50 =1/х
100+2(х+15) 1
= избавимся от знаменателей
2*(х+15)*100 х
х*(130+2х) =1*2*(х+15)*100
130х+2х²=200х+3000
2х²-70х-3000=0 /2
х²-35х-1500=0
D=1225+6000=7225 √D=85
x=(35+85)/2=60 км/ч
х=(35-85)/2=-25 не подходит
ответ : скорость первого автомобиля 60 км/ч
ответ: 24 км/ч.
Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила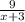 часов и против течения реки, на расстояние в 14 км, лодки затратила
часов и против течения реки, на расстояние в 14 км, лодки затратила 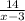 часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это
часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это 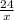 часов. Составим уравнение:
часов. Составим уравнение:
x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.
x₂=24 (км/ч) скорость лодки в стоячей воде.