1. Сложение векторов AB + BC определяется из правила параллелограмма.
Путем параллельного переноса соединить начала обоих векторов в одной точке, достроить до параллелограмма. Диагональ параллелограмма является суммой двух векторов
Диагонали в точке пересечения M делятся пополам, т.е.
2) Длину вектора ВС можно найти по теореме Пифагора из прямоугольного треугольника ABM, в нем |BM|=|BD|/2 = 8 см; |AM| = 6 см
см
3) Для начала найдем координаты вектора АС:
2. 1) Координаты вектора АС:
Длина вектора АС: см
2) Координаты вектора BD:
Длина вектора BD: см
3.CT || AM || BP как перпендикулярны к одной прямой, значит четырехугольник AMTC - прямоугольная трапеция, BP - средняя линия трапеции, следовательно
1. Сложение векторов AB + BC определяется из правила параллелограмма.
Путем параллельного переноса соединить начала обоих векторов в одной точке, достроить до параллелограмма. Диагональ параллелограмма является суммой двух векторов
Диагонали в точке пересечения M делятся пополам, т.е.
2) Длину вектора ВС можно найти по теореме Пифагора из прямоугольного треугольника ABM, в нем |BM|=|BD|/2 = 8 см; |AM| = 6 см
3) Для начала найдем координаты вектора АС:
2. 1) Координаты вектора АС: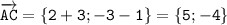
Длина вектора АС: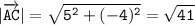 см
см
2) Координаты вектора BD: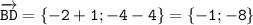
Длина вектора BD: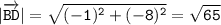 см
см
3.CT || AM || BP как перпендикулярны к одной прямой, значит четырехугольник AMTC - прямоугольная трапеция, BP - средняя линия трапеции, следовательно
Даны координаты вершины треугольника ABC :А(1;0) ,В(13;-19),С(17;13) найти уравнение стороны АВ и АС и их угловые коэффициенты.
Находим векторы.
АВ = В(13;-19) - А(1;0) = (12; -19). По координатам вектора сразу определяется угловой коэффициент прямой АВ.
к(АВ) = Δу/Δх = -19/12.
Уравнение АВ: (x- 1)/12 = y/(-19) каноническое, или
19x + 12y - 19 = 0 общего вида, или
у = (-19/12)х + (19/12) с угловым коэффициентом.
АС = С(17;13) - А(1;0) = (16; 13). По координатам вектора сразу определяется угловой коэффициент прямой АС.
к(АС) = Δу/Δх = 13/16.
Уравнение АС: (x- 1)/16 = y/13) каноническое, или
13x - 16y - 13 = 0 общего вида, или
у = (13/16)х - (13/16) с угловым коэффициентом.