побудуйте графік функцій f (x)=-x*+6х-5
укажіть:
б) нулі функції;
в) координати вершини;
г) значеннях для яких у> 0, у< 0;
д) проміжки зростання і спадання функції;
е) найбільше (найменше) значення функції.​

x^2 - 3x + 2 = (x - 1)(x - 2) < 0

Решением этого неравенства является промежуток (1, 2)

Разложим на множители левую часть второго неравенства:

ax^2 - (3a + 1)x + 3 = (ax^2 - x) - (3ax - 3) = x(ax - 1) - 3(ax - 1) = (x - 3)(ax - 1) = a(x - 3)(x - 1/a)

Возможны 5 вариантов.

1) a > 1/3. Тогда решение неравенства – промежуток (1/a, 3). Нужно, чтобы промежуток (1, 2) полностью содержался в нём, так будет, если 1/a < 1. Объединяем с условием a > 1/3 и получаем часть ответа: a > 1.

2) a = 1/3. У второго неравенства нет решений.

3) 0 < a < 1/3. Решение неравенства – промежуток (3, 1/a); такой промежуток никогда не содержит (1, 2).

4) a = 0. Второе неравенство превращается в 3 - x < 0, x > 3. Не подходит.

5) a < 0. Решение второго неравенства – промежуток (1/a, 3), при этом 1/a < 0. Подходит.

ответ.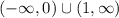

-x^2 +3x-1  >=  0
x^2 -3x+1   =<  0
разложим на множители
x^2 -3x+1   =  0
D = (-3)^2 - 4*1*1=5
x = 1/2 (3 +/- √5)
x1 = (3 - √5)/2
x2 = (3 + √5)/2
(x-x1) (x-x2) = (x-(3 - √5)/2) (x-(3 + √5)/2) =1/2 ([2x- 3] + √5) 1/2 ([2x-3] - √5) =
= 1/4 ([2x- 3] + √5)([2x-3] - √5)
решим неравенство
1/4 ([2x- 3] + √5)([2x-3] - √5) =<0
система А
([2x- 3] + √5) =< 0 ; x =< (3 - √5) /2 
([2x-3] - √5)  >=0 ;  x >= (3 + √5) /2 
не имеет решений
система В
([2x- 3] + √5) >= 0 ; x >= (3 - √5) /2 
([2x-3] - √5)  =<  0 ;  x =<  (3 + √5) /2 
решение системы    (3 - √5) /2   x =<  (3 + √5) /2 
ОТВЕТ  [ (3 - √5) /2 ; (3 + √5) /2   ]