Побудуйте в одній системі координат графіки лінійних функцій:
у=3; у=-4; у=0

Здравствуйте, Sonya2006f!

Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.

Разложение чисел на простые множители:

Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.

Формула сокращённого умножения:

НЕПОЛНЫЙ КВАДРАТ СУММЫ:  .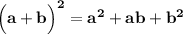

Зная, что первоначально выражение имело вид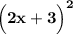   , перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.

Разложение данного выражения на множители:

Окончательный ответ данной задачи:

Неполный квадрат суммы данного выражения - "6x".

С Уважением, NeNs07.

1) х²-3х-40>0

D=(-(-3))²-4×1×(-40)=9+169=169

x1=(-(-3)-√169)/2×1=(3-13)/2=-5

x2=(-(-3)+√169)/2×1=(3+13)/2=16/2=8

x∈(-∞;-5)и(8;+∞)

х⁺(-5)--₋(8)--⁺---х

2) х²>-5х+14

х²+5х-14>0

По теореме Виета:

х₁+х₂=-5

х₁×х₂=-14

х₁=-7

х₂=2

х---⁺---(-7)---₋---(2)---⁺---х

х∈(-∞;-7) и (2;+∞).

3) 10х²+2х+34>4х²-х+79

10х²+2х+34-4х²+х-79>0

6х²+3х-45>0

D=(-3)²-4×6×(-45)=9+1080=1089

x₁=(-3-√1089)/2×6=(-3-33)/12=-36/12=-3

x₂=(-3+√1089)/2×6=(-3+33)/12=30/12=5/2=2,5

x---⁺---(-3)---₋---(2,5)---⁺---x

x ∈(-∞;-3) и (2,5;+∞).

4) 2х²+14х-20>(х-6)²

2х²+14х-20-(х²-12х+36)>0

2х²+14х-20-х²+12х-36>0

х²+26х-56>0

D=(-26)²-4×1×(-56)=676+224=900

x₁=(-26-√900)/2×1=(-26-30)/2=-56/2=-28

x₂=(-26+√900)/2×1=(-26+30)/2=4/2=2

x---⁺---(-28)---₋---(2)---⁺---x

x∈(-∞;-28) и (2;+∞).