Подберите одночлены А, B,C так, чтобы выполнялись равенство
(2х+3у)(А-В+С)=8х3 + 27у3

порядок числа Х равен  6

число Х  имеет вид  а * 10⁶ , где  1 ≤ а < 10

а) х²  =   ( а * 10⁶)²  = а² * 10¹²   (порядок 12)

в данном выражении      1² ≤ а² < 10²

                                         1 ≤ а² < 100   , 

это значит, что   а²  может принимать значения не только от 1 до 10, 

но и  в промежутке [10; 100), что увеличивает порядок числа ещё на 1,

т.е. порядок будет 12 + 1 = 13.

 Значит порядок числа х² может быть 12 или 13.

б) х⁵  =   ( а * 10⁶)⁵ = а⁵ * 10³⁰   (порядок 30)

в данном выражении      1⁵ ≤ а⁵ < 10⁵

                                         1 ≤ а⁵ < 10⁵   , 

это значит, что   а²  может принимать значения не только от 1 до 10, 

но и в промежутке [10; 10⁵), что может увеличить порядок числа максимум ещё на 4,  т.е. порядок максимум может быть 30 + 4 = 34

 Значит порядок числа х² может быть  равен 30, 31, 32, 33 или 34.

в)  √х = х¹/² = ( а * 10⁶)¹/² = а¹/² * 10³

  в данном выражении      1¹/² ≤ а¹/² < 10¹/²

                                          1 ≤ а¹/² <  10¹/²

т.о.  а¹/²  удовлтворяет стандартной записи числа, т.е .лежит в промежутке

от 1 включительно до 10.

 Значит порядок числа √х равен  3.

г) 1/х  = х⁻¹ = ( а * 10⁶)⁻¹ = а⁻¹ * 10⁻⁶ = 1/а* 10⁻⁶  (порядок равен -6)

   т.к.     1 ≤ а < 10     =>  1/10 < 1/а ≤ 1    =>   

это значит, что   1/а   может принимать значения не только = 1, 

но и в промежутке (1/10; 1], что может уменьшить порядок числа на 1.

Значит порядок числа 1/х  может быть  равен -6   или -7.

Пусть первоначальная скорость равна х км/ч, а после увеличения скорости - (x+12) км/ч. Время пути из пункта А в пункт В, равно 300/х ч, а из пункта В в пункт А - 300/(x+12) ч. На обратный путь автомобиль затратил на 50 мин меньше, чем на путь от А до В, значит составляем и решим уравнение

50 мин = 50/60 ч = 5/6 ч.

По теореме Виета

— не удовлетворяет условию.

км/ч - первоначальная скорость автомобиля.

ответ: 60 км/ч.

2) Найдем дискриминант квадратного уравнения

D>0 для всех действительных k имеет два действительных корня, значит нет такого значения k в котором квадратное уравнение имело бы только один корень.

3) Квадратное уравнение имеет корни(т.к.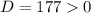 ), значит можем воспользоваться теоремой Виета.