1)
очевидна справедливость неравенства.
2)
3)
4)
1) Доказать, что 3,4 < √12 < 3,6
Доказательство;
11,56 < 12 < 12,96
Функция у = √х возрастающая, тогда
√11,56 < √12 < √12,96, т.е.
3,4 < √12 < 3,6, что и требовалось доказать.
2) Доказать, что 5 < √30 < 6
25 < 30 < 36
√25 < √30 < √36, т.е.
5 < √30 < 6, что и требовалось доказать.
3) Доказать, что 5 < √26 < 5,1
25 < 26 < 26,01
√25 < √26 < √26,01, т.е.
5 < √26 < 5,1, что и требовалось доказать.
4) Доказать, что 7.9 < √63 < 8
62,41 < 63 < 64
√62,41 < √63 < √64 т.е.
7,9 < √63 < 8, что и требовалось доказать
1)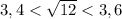
2)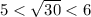
3)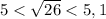
4)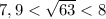
1) Доказать, что 3,4 < √12 < 3,6
Доказательство;
11,56 < 12 < 12,96
Функция у = √х возрастающая, тогда
√11,56 < √12 < √12,96, т.е.
3,4 < √12 < 3,6, что и требовалось доказать.
2) Доказать, что 5 < √30 < 6
Доказательство;
25 < 30 < 36
Функция у = √х возрастающая, тогда
√25 < √30 < √36, т.е.
5 < √30 < 6, что и требовалось доказать.
3) Доказать, что 5 < √26 < 5,1
Доказательство;
25 < 26 < 26,01
Функция у = √х возрастающая, тогда
√25 < √26 < √26,01, т.е.
5 < √26 < 5,1, что и требовалось доказать.
4) Доказать, что 7.9 < √63 < 8
Доказательство;
62,41 < 63 < 64
Функция у = √х возрастающая, тогда
√62,41 < √63 < √64 т.е.
7,9 < √63 < 8, что и требовалось доказать