Найти по одному решению каждого уравнения - не проблема. А вот найти все натуральные решения - это намного более сложная задача.
Простейшие решения в первой задаче (1;1)), во второй (3;2), в третьей (1;1). Дальше можете не смотреть (а можете посмотреть).
1) Преобразуем так: (x²-1)(y²-1)=0; x²-1=0 или y²-1=0; x=1 или y=1.
То есть решения такие: (1;1), (1;2), (1;3), ..., (2;1), (3;1),...
2) Преобразуем так: x²-2y²=1. Это намного более сложная задача - частный случай так называемого уравнения Пелля. Заинтересуетесь - почитайте литературу на эту тему, только сначала попробуйте решить сами. Годится, как я уже писал, пара (3;2), остальные пары получаются из этой по такому правилу: если была пара (x;y), то следующая равна (3x+4y;2x+3y). Поэтому получаем второе решение (3·3+4·2;2·3+3·2)=(17;12). Можете построить сколько угодно решений по такому правилу.
3) Конечно, если m=n, то Поэтому мы уже имеем бесконечное множество решений. Но ими множество решений не исчерпывается. По крайней мере то есть получили решения (2;4) и (4;2). Докажем, что других решений нет. Преобразуем так:
Рассмотрим функцию (x≥1)
Слева от e производная положительна, справа отрицательна, то есть слева от e функция возрастает, справа убывает.
при этом все эти числа кроме f(1) больше 1. Поэтому кроме f(2)=f(4) все эти числа разные.
ответ в третьей задаче: (2;4), (4;2), (1;1), (2;2), (3;3),...
прощения, если не все было понятно - в будущем разберетесь))
2) Тогда (х + 7) см — длина большего катета.
3) По теореме Пифагора в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы, поэтому:
х^2 + (x + 7)^2 = 13^2.
4) Решим уравнение:
х^2 + x^2 + 14x + 49 = 169;
2x^2 + 14x + 49 - 169 = 0;
2x^2 + 14x - 120 = 0;
х^2 + 7x - 60 = 0.
По теореме Виета находим: х1 = -12, х2 = 5.
5) х1 = -12 не может являться решением задачи.
6) х = 5 см — длина одного катета.
7) 5 + 7 = 12 см — длина второго катета.
ответ: 12 и 5 см.
Найти по одному решению каждого уравнения - не проблема. А вот найти все натуральные решения - это намного более сложная задача.
Простейшие решения в первой задаче (1;1)), во второй (3;2), в третьей (1;1). Дальше можете не смотреть (а можете посмотреть).
1) Преобразуем так: (x²-1)(y²-1)=0; x²-1=0 или y²-1=0; x=1 или y=1.
То есть решения такие: (1;1), (1;2), (1;3), ..., (2;1), (3;1),...
2) Преобразуем так: x²-2y²=1. Это намного более сложная задача - частный случай так называемого уравнения Пелля. Заинтересуетесь - почитайте литературу на эту тему, только сначала попробуйте решить сами. Годится, как я уже писал, пара (3;2), остальные пары получаются из этой по такому правилу: если была пара (x;y), то следующая равна (3x+4y;2x+3y). Поэтому получаем второе решение (3·3+4·2;2·3+3·2)=(17;12). Можете построить сколько угодно решений по такому правилу.
3) Конечно, если m=n, то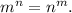
Поэтому мы уже имеем бесконечное множество решений. Но ими множество решений не исчерпывается. По крайней мере 
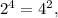то есть получили решения (2;4) и (4;2). Докажем, что других решений нет. Преобразуем так: ![\sqrt[m]{m}=\sqrt[n]{n}.](/tpl/images/4529/0693/329fd.png)
Рассмотрим функцию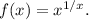
(x≥1)
Слева от e производная положительна, справа отрицательна, то есть слева от e функция возрастает, справа убывает.
ответ в третьей задаче: (2;4), (4;2), (1;1), (2;2), (3;3),...
прощения, если не все было понятно - в будущем разберетесь))