Пользуюсь определением понятие больше и меньше для чисел сравните a и b если известно что а) a-b= -3 б) b-a=0,01 в) a-b=(-8)2 2 сверху г)b-a=0

Дано: ABC - равнобедренный треугольник; AC = 12 см; AD = 9.6 см; AB=BC.

Найти: Рabc.

Из прямоугольного треугольника ADC по теореме Пифагора найдем CD

см.

Пусть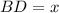 , тогда .

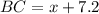Рассмотрим прямоугольный треугольник BHC найдем высоту BH к стороне основания AC; AH=CH=AC/2=6 см.

Площадь равнобедренного треугольника равна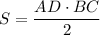 , с другой стороны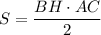

Приравнивая площади, получим AD * BC = BH * AC.

После возведения в квадрат обе части уравнения и упрощений с подобными членами вы должны получить следующее квадратное уравнение

Корни которого: - не удовлетворяет условию

                                см

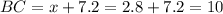Тогда см

Pabc = AB + BC + AC = 10 + 10 + 12 = 32 см

ответ: 32 см.

Формулы для квадратов (a
+ b
)2 = a
2 + 2ab
+ b
2– квадрат суммы (a
– b
)2 = a
2 – 2ab
+ b
2– квадрат разностиa
2 – b
2 = (a
– b
)(a
+ b
)– разность квадратов (a
+ b
+ c
)2 = a
2 + b
2 + c
2 + 2ab
+ 2ac
+ 2bc
Формулы для кубов (a
+ b
)3 = a
3 + 3a
2b
+ 3a
b
2 + b
3– куб суммы (a
– b
)3 = a
3 – 3a
2b
+ 3a
b
2 – b
3– куб разностиa
3 + b
3 = (a
+ b
)(a
2 – ab
+ b
2)– сумма кубовa
3 – b
3 = (a
– b
)(a
2 + ab
+ b
2)– разность кубов
Формулы для четвёртой степени (a
+ b
)4 = a
4 + 4a
3b
+ 6a
2b
2 + 4a
b
3 + b
4(a
– b
)4 = a
4 – 4a
3b
+ 6a
2b
2 – 4a
b
3 + b
4a
4 – b
4 = (a
– b
)(a
+ b
)(a
2 + b
2)
Формулы для n
-той степени (a
+ b
)n
= an
+ na
n
– 1b
+ n
(n
– 1)a
n
– 2b
2 + ..+ n
!an – kbk
+ ..+ bn
2k
!(n – k
)!(a
– b
)n
= an
– na
n
– 1b
+ n
(n
– 1)a
n
– 2b
2 + ..+ (-1)k
n
!an – kbk
+ ..+ (-1)nbn
2k
!(n – k
)!