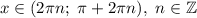В двух строчках у Вас несколько ошибок математических. Во-первых, функция.ю скорее всего, у = 8х - 10, а не то, что написано. И во-вторых, точки пересечения, как я понимаю, с осями? Если я правильно поняла, то вот решение. Чтобы найти точки пересечения функции с осями, надо решить системы уравнений данной функции (в моем варианте, т.к. в Вашем варианте у = -2 получается постоянная функция, которая параллельна оси Х и, следовательно, не пересекается с ОХ) с уравнениями осей. Найдем точку пересечения данной функции с осью Х, уравнение которой у=0: у = 8х - 10 у = 0
8х - 10 = 0 х = 10/8 = 5/4 Точка пересечения с осью Х имеет координаты (5/4, 0) Точно так же наудем точку пересечения нашего графика с осью У, уравнение которой х = 0: у = 8х - 10 х = 0 у = -10
Точка пересечения данного графика с осью У (0, -10)
Произведение двух выражений будет отрицательно, если они имеют разные знаки. Запишем совокупность двух систем:
Рассмотрим из второй системы неравенство . Оно не имеет решений, так как синус принимает значения из отрезка . Значит, и вся вторая система не имеет решений.
В рассмотрении остается первая система, решения которой будут соответствовать решениям совокупности:
Рассмотрим неравенство . Оно напротив выполняется при любых значениях по тем же причинам: синус принимает значения из отрезка .
Тогда, решение системы сводится к решению первого неравенства:
Найдем точку пересечения данной функции с осью Х, уравнение которой у=0:
у = 8х - 10
у = 0
8х - 10 = 0
х = 10/8 = 5/4
Точка пересечения с осью Х имеет координаты (5/4, 0)
Точно так же наудем точку пересечения нашего графика с осью У, уравнение которой х = 0:
у = 8х - 10
х = 0 у = -10
Точка пересечения данного графика с осью У (0, -10)
Произведение двух выражений будет отрицательно, если они имеют разные знаки. Запишем совокупность двух систем:
Рассмотрим из второй системы неравенство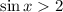 . Оно не имеет решений, так как синус принимает значения из отрезка
. Оно не имеет решений, так как синус принимает значения из отрезка ![[-1;\ 1]](/tpl/images/4675/5711/c3b68.png) . Значит, и вся вторая система не имеет решений.
. Значит, и вся вторая система не имеет решений.
В рассмотрении остается первая система, решения которой будут соответствовать решениям совокупности:
Рассмотрим неравенство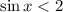 . Оно напротив выполняется при любых значениях
. Оно напротив выполняется при любых значениях  по тем же причинам: синус принимает значения из отрезка
по тем же причинам: синус принимает значения из отрезка ![[-1;\ 1]](/tpl/images/4675/5711/c3b68.png) .
.
Тогда, решение системы сводится к решению первого неравенства:
ответ: