Помагите решить задания .
Исследовать Функ.на:а)монотонность и экстремум
б)наибольшее и наименьшее значения на заданном отрезке

геометричної прогресії. Позначимо члени зростаючої прогресії через a-d, a, a+d. Тоді їх сума рівна 3a=21, звідки a=21/3=7. Отже середній член арифметичної прогресії відомий. Тепер знайдемо члени геометричної прогресії

Перший – a-d+2=7-d+2=9-d

другий a+3=7+3=10.

третій a+d+9=7+d+9=16+d.

За властивістю геометричної прогресії квадрат середнього її члена рівний добутку рівновіддалених, тобто

геометрична прогресія, формули

Підставимо члени геометричної прогресії у формулу

(9-d)(16+d)=10^2=100.

Розкриємо дужки та зведемо до квадратного рівняння відносно різниці арифметичної прогресії.

квадратне рівняння

Знаходимо дискримінант

дискримінант

та крок арифметичної прогресії

крок арифметичної прогресії

Більший член арифметичної прогресії рівний

a+d=7+4=11.

Ось такі складні завдання на прогресію Вам можуть зустрітися у навчанні

Объяснение:

Однозначно (-∞; ) ∪ (; +∞).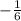

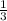Понравился ответ? Жду лайк и 5 звезд! )))

Объяснение:

Выражение, находящееся под корнем, не может быть отрицательным. К тому же, сам корень, находясь в знаменателе, не может быть равен нулю. Объединяя эти два условия, имеем:

Корни в скобках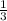 и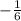

На координатной прямой это выглядело бы так:

+                                       -                        +

--------------------o------------------------o----------------------->

Корни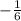                                      

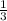
Знаки "+" стоят на промежутках (-∞;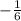 ) ∪ (; +∞).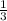