(x^2 - 0.75)^2 + 1 < 0 - не может быть ни при каких x, потому что значение выражения (x^2 - 0.75)^2 + 1 всегда положительно, значит, f(x) не будет больше g(x) ни при каких значениях x.
б) График функции y = f(x) находится ниже графика функции y =g(x), значит, выполняется неравенство f(x) < g(x)
Объяснение:
a) По условию составляем неравенство
-2x^2 + 2x -3 > -x -1
-2x^2 + 3x -2 > 0
2x^2 - 3x + 2 < 0
x^2 - 1.5x + 1 < 0
(x^2 - 0.75)^2 + 1 < 0 - не может быть ни при каких x, потому что значение выражения (x^2 - 0.75)^2 + 1 всегда положительно, значит, f(x) не будет больше g(x) ни при каких значениях x.
б) График функции y = f(x) находится ниже графика функции y =g(x), значит, выполняется неравенство f(x) < g(x)
x/3 < 6/x
x/3 - 6/x < 0
(x^2 - 18)/3x < 0
1.
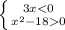3x < 0 ⇒ x<0 ⇒ x < -
(x +
)(x - 
) > 0 ⇒ x < -
или x>
2.
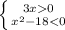3x > 0 ⇒ x>0
(x +
)(x - 
) < 0 ⇒ x < 
и x>-
⇒ 0<x < 
x < -
и 0<x < 
Упростим выражение.
Сначала нам с тобой нужно перемножить выражение в скобках. давай сделаем это.
Умножаем каждый член из первого выражения в скобках, на каждый член второго выражения в скобках
значит
-(3a-2ab+3*3-3*2b)
умножим и вычислим произведение.
-(3а-2ab+9-6b)
значит
получим
2ab-3a+2b-3a-(a+3)*(3-2b)
Когда перед скобками стоит знак -, изменим знак каждого члена в скобках
2ab-3a+2b-3-3а+2ab-9+6b
далее нам нужно сгруппировать подобные члены сложением их коэфицентов,
то есть из 2ab+2ab
получаетСя 2+2(ab)
что в итоге будет 4(ab)
тоже повторим и с другим.
-3а-3а
значит
(-3-3)а
значит
-6а
и тоже самое с последним
2b+6b
(2+6)b
8b
и наконец вынесем знак минус за скобки
-3-9
значит
-(3+9)
значит -12.
И мы справились! выражение успешно упростили!
Получим ответ
4ab-6a+8b-12