понять доказательство утверждения! пример 6 - на стр. 17 написано «для самого числа а есть три » - далее перечисляются варианты. не могу понять, почему именно эти объясните досконально, как ребёнку. давно сижу, не могу догадаться
а) Выбрать 4 ромашки можно а 3 незабудки - По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно
ответ
b) Как минимум 4 незабудки это 4 незабудки или 5 незабудки или 6 незабудки или 7 незабудки.. Чувствуется что здесь правило сложения. Четыре незабудки и три ромашки можно Выбрать пять незабудки и две ромашки можно Выбрать шесть цветов незабудки и одна ромашку можно И наконец выбрать семь цветов незабудки можно По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
попытаюсь объяснить. в целом алгоритм простой. легче всего, конечно, построить график и посмотреть где функция убывает, а где возрастает. Но если такой не подходит, то надо искать производную. В первом примере производная от синуса равна косинусу. Приравняем получившуюся производную к нулю (f'(x)=cosx=0). То есть х=π/2+πn, где n∈Z. Именно при таких х производная равна 0, то есть функция f(x) меняет свою монотонность. Если производная меньше нуля, то функция убывает, если больше, то она возрастает. Для этого надо подставить какие нибудь значения справа и слева от точек x=π/2+πn. Получаем что слева функция возрастает, а справа убывает. То есть функция возрастает от -π/2+πn, до π/2+πn, а убывает от π/2+πn до 3π/2+πn, где n∈Z.
Аналогично решим и другие. (надеюсь что теорию вы поняли, поэтому не буду расписывать)
2) Производная от косинуса равна минус синусу. Синус равен нулю в точках πn, где n∈Z. Так как при π/2 -sin(π/2) <0, то на промежутке от 0+πn до π+πn, где n ∈Z, функция убывает (так как точка π/2 лежит на таком промежутке при n=0 ), значит на интервале от -π+πn до 0+πn функция возрастает.
3) производная от тангенса равна 1/((cos x)^2). То есть при любых х производная больше 0. Это значит что функция возрастает на всей области определения.
4) производная от данной функции равна f'(x)=2cos(2x)-2sin(2x). Производная равна нулю при x=π/8+2πn и x=5π/8+2πn, где n∈Z. Решив аналогично предыдущим примерам, получим, что функция убывает на интервале [π/8+2πn; 5π/8+2πn] и возрастает на интервале [5π/8+2πn; 9π/8+2πn] где n∈Z.
а) Выбрать 4 ромашки можно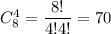 а 3 незабудки -
а 3 незабудки - 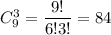 По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно
По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно 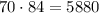
ответ
b) Как минимум 4 незабудки это 4 незабудки или 5 незабудки или 6 незабудки или 7 незабудки.. Чувствуется что здесь правило сложения. Четыре незабудки и три ромашки можно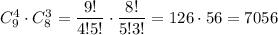 Выбрать пять незабудки и две ромашки можно
Выбрать пять незабудки и две ромашки можно 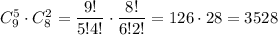 Выбрать шесть цветов незабудки и одна ромашку можно
Выбрать шесть цветов незабудки и одна ромашку можно 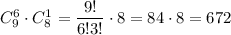 И наконец выбрать семь цветов незабудки можно
И наконец выбрать семь цветов незабудки можно 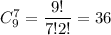 По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
ответ: 11292.
Объяснение:
попытаюсь объяснить. в целом алгоритм простой. легче всего, конечно, построить график и посмотреть где функция убывает, а где возрастает. Но если такой не подходит, то надо искать производную. В первом примере производная от синуса равна косинусу. Приравняем получившуюся производную к нулю (f'(x)=cosx=0). То есть х=π/2+πn, где n∈Z. Именно при таких х производная равна 0, то есть функция f(x) меняет свою монотонность. Если производная меньше нуля, то функция убывает, если больше, то она возрастает. Для этого надо подставить какие нибудь значения справа и слева от точек x=π/2+πn. Получаем что слева функция возрастает, а справа убывает. То есть функция возрастает от -π/2+πn, до π/2+πn, а убывает от π/2+πn до 3π/2+πn, где n∈Z.
Аналогично решим и другие. (надеюсь что теорию вы поняли, поэтому не буду расписывать)
2) Производная от косинуса равна минус синусу. Синус равен нулю в точках πn, где n∈Z. Так как при π/2 -sin(π/2) <0, то на промежутке от 0+πn до π+πn, где n ∈Z, функция убывает (так как точка π/2 лежит на таком промежутке при n=0 ), значит на интервале от -π+πn до 0+πn функция возрастает.
3) производная от тангенса равна 1/((cos x)^2). То есть при любых х производная больше 0. Это значит что функция возрастает на всей области определения.
4) производная от данной функции равна f'(x)=2cos(2x)-2sin(2x). Производная равна нулю при x=π/8+2πn и x=5π/8+2πn, где n∈Z. Решив аналогично предыдущим примерам, получим, что функция убывает на интервале [π/8+2πn; 5π/8+2πn] и возрастает на интервале [5π/8+2πn; 9π/8+2πn] где n∈Z.