1)
Находим все точки на окружности, у которых косинус = 1
Это право единичной окружности. Значение повторяется каждый круг. Значит все точки задаются выражением
n везде целое
2) Аналогично. Ищем точки у которых косинус = -1
Это лево окружности
n всё ещё целое (но это уже не n из 1 примера, а очевидно другое)
3) cos чего-то равен 0. Значит это что-то =
n целое
1)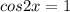
Находим все точки на окружности, у которых косинус = 1
Это право единичной окружности. Значение повторяется каждый круг. Значит все точки задаются выражением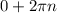
n везде целое
2) Аналогично. Ищем точки у которых косинус = -1
Это лево окружности
3) cos чего-то равен 0. Значит это что-то =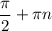
n целое