Допустим в банк вложили Х рублей под 10% годовых .Через год насчету станет 1,1x руб. Если бы Пётр ничего не снимал со счёта, то через год там оказалось бы 1,1²x руб, а спустя три года оказалось бы 1,1³x руб . Но так как он снял через год n рублей , то на счету стала сумма 1,1x - n , ещё через год (1,1x - n) * 1,1. Через год Пётр снова кладёт на счёт 100 000 рублей и на счёте оказывается сумма (1,1x - n) * 1,1 + 100 000 . Через три года на счету [(1,1x - n) * 1,1 + 100 000] * 1,1 = 1,1³x - n * 1,1² + 100 000 * 1,1 = = 1,1³x - n * 1,1² +110 000 Сумма 1,1³x больше суммы 1,1³x - n * 1,1² + 110 000 на 4950 1,1³x - 11³ x + n * 1,1² - 110 000 = 4950 n * 1,1² = 114 950 n = 95 000 Пётр снял 95 000 рублей
Через три года на счету
[(1,1x - n) * 1,1 + 100 000] * 1,1 = 1,1³x - n * 1,1² + 100 000 * 1,1 =
= 1,1³x - n * 1,1² +110 000
Сумма 1,1³x больше суммы 1,1³x - n * 1,1² + 110 000 на 4950
1,1³x - 11³ x + n * 1,1² - 110 000 = 4950
n * 1,1² = 114 950
n = 95 000
Пётр снял 95 000 рублей
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение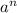
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение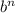
.
Рассмотрим многочлен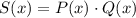
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена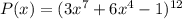
:
- степень определяется выражением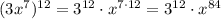
, то есть степень равна 84
- свободный член равен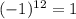
Для многочлена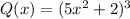
:
- степень определяется выражением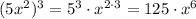
, то есть степень равна 6
- свободный член равен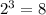
Наконец, для многочлена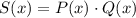
получим:
- степень определяется выражением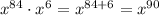
, то есть степень равна 90
- свободный член равен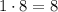
Сумма степени и свободного члена многочлена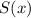
:
ответ: 98