Постарайся ответить, не выполняя построение на координатной плоскости! 1. Один конец отрезка находится в начальной точке координатной системы о(0; 0).
Другой конец А имеет координаты (20; 0).
Определи координаты серединной точки с отрезка ОА.
с (D: O).
2. Один конец отрезка находится в начальной точке координатной системы о(0; 0).
Другой конец В имеет координаты (0; 10).
Определи координаты серединной точки D отрезка ов.
D(О;
3. Один конец отрезка находится в точке М с координатами (20; 10), другой конец N имеет координаты (2; 34).
Определи координаты серединной точки К отрезка MN.
к (р; ).
Сколько их?
а₁=1; a₂=3 => d=a₂-a₁=3-1=2
a(n)=99
a(n)=a₁+d(n-1)
1+2(n-1)=99
2(n-1)=98
n-1=49
n=50 - количество нечётных чисел меньших 100
{3;9;15;...;99} - множество нечётных чисел кратных числу 3 и меньших 100
Сколько их?
a₁=3, a₂=9 => d=a₂-a₁=9-3=6
a(m)=99
a(m)=a₁+d(m-1)
3+6(m-1)=99
6(m-1)=96
m-1=16
m=17 - количество нечётных чисел кратных числу 3 и меньших 100
{5;15;25;...;95} - множество нечётных чисел кратных числу 5 и меньших 100
а₁=5; а₂=15 => d=a₂-a₁=15-5=10
a(p)=a₁+d(p-1)
5+10(p-1)=95
10(p-1)=90
p-1=9
p=10 - количество нечётных чисел кратных числу 5 и меньших 100
Среди нечётных чисел кратных числам 3 и 5 одновременно встречаются числа 15; 45 и 75 (всего их 3)
Общее количество нечётных натуральных чисел, делящихся на 3 или на 5:
m+p-3=17+10-3=24
Количество нечётных натуральных чисел, которые не делятся ни на 3, ни на 5 равно: 50-24=26
ответ: 26
х мальчиков в классе
у девочек в классе
3х/5 мальчиков изучают английский язык
3у/7 девочек изучают английский язык
2х/5 мальчиков изучают немецкий язык
4у/7 девочек изучают немецкий язык
По условию
(3х/5 + 3у/7) > (2х/5 + 4у/7) на 2
Получаем уравнение:
По условию
25 < (x+y) < 36 => (x+y) ∈ (25; 36)
Далее решаем методом подбора.
1) Пусть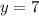
, тогда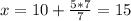 
х=15; у=7
(х+у) = 7+15=22 ∉ (25; 36)
2) Пусть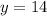
, тогда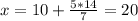 
х=20; у=14
(х+у) = 14+20=34 ∈ (25; 36)
Получаем:
20 мальчиков в классе
14 девочек в классе
20-14 = 6
В классе на 6 мальчиков больше, чем девочек.
ответ под буквой А. Мальчиков, на 6.