210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть , где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов:
Умножить оба уравнения на 2, чтобы избавиться от дроби:
х - у = 10
3х - у = 22
Преобразовать уравнения в уравнения функции:
х - у = 10 3х - у = 22
-у = 10 - х -у = 22 - 3х
у = х - 10 у = 3х - 22
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблицы:
х -1 0 1 х -1 0 1
у -11 -10 -9 у -25 -22 -19
Согласно графиков, координаты точки пересечения (6; -4).
Решение системы уравнений (6; -4).
4) (х - у)/4 = 1
3(х + у)/4 = 3
Умножить оба уравнения на 4, чтобы избавиться от дроби:
х - у = 4
3х + 3у = 12
Преобразовать уравнения в уравнения функции:
х - у = 4 3х + 3у = 12
-у = 4 - х 3у = 12 - 3х
у = х - 4 у = (12 - 3х)/3
у = 4 - х
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблицы:
х -1 0 1 х -1 0 1
у -5 -4 -3 у 5 4 3
Согласно графиков, координаты точки пересечения (4; 0).
210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть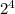
, где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов:
В решении.
Объяснение:
Решить графически систему уравнений:
3) х/2 - у/2 = 5
3х/2 - у/2 = 11
Умножить оба уравнения на 2, чтобы избавиться от дроби:
х - у = 10
3х - у = 22
Преобразовать уравнения в уравнения функции:
х - у = 10 3х - у = 22
-у = 10 - х -у = 22 - 3х
у = х - 10 у = 3х - 22
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблицы:
х -1 0 1 х -1 0 1
у -11 -10 -9 у -25 -22 -19
Согласно графиков, координаты точки пересечения (6; -4).
Решение системы уравнений (6; -4).
4) (х - у)/4 = 1
3(х + у)/4 = 3
Умножить оба уравнения на 4, чтобы избавиться от дроби:
х - у = 4
3х + 3у = 12
Преобразовать уравнения в уравнения функции:
х - у = 4 3х + 3у = 12
-у = 4 - х 3у = 12 - 3х
у = х - 4 у = (12 - 3х)/3
у = 4 - х
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблицы:
х -1 0 1 х -1 0 1
у -5 -4 -3 у 5 4 3
Согласно графиков, координаты точки пересечения (4; 0).
Решение системы уравнений (4; 0).