Алгебра: Построить график функции

Построить график функции

Показать ответ

Ответ:

11SOS11

27.08.2021 14:05

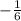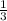Однозначно (-∞; $-\frac{1}{6}$ ) ∪ ( $\frac{1}{3}$ ; +∞).

Понравился ответ? Жду лайк и 5 звезд! )))

Объяснение:

Выражение, находящееся под корнем, не может быть отрицательным. К тому же, сам корень, находясь в знаменателе, не может быть равен нулю. Объединяя эти два условия, имеем:

(3x-1)(6x+1)0

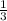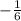
Корни в скобках $\frac{1}{3}$ и $-\frac{1}{6}$

На координатной прямой это выглядело бы так:

+ - +

--------------------o------------------------o----------------------->

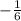
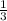
Корни $-\frac{1}{6}$ $\frac{1}{3}$

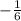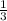Знаки "+" стоят на промежутках (-∞; $-\frac{1}{6}$ ) ∪ ( $\frac{1}{3}$ ; +∞).

0,0(0 оценок)

Ответ:

Kamjla1

06.12.2022 17:36

Вообще область значений тангенса и котангенса - все действительные числа:

$E(\mathrm{tg}x)=E(\mathrm{ctg}x)=(-\infty;\ +\infty)$

а)

$y=|\mathrm{tg}x|$

Если рассмотреть модуль тангенса, то отрицательные значения примут противоположные значения, то есть станут положительными. Нулевое и положительные значения сохранятся. Получим область значений:

$E(|\mathrm{tg}x|)=[0;\ +\infty)$

б)

$y=\mathrm{ctg}^2x$

Котангенс может принять значение любого действительного числа, но при возведении любого числа в квадрат результат получится неотрицательным.

$E(\mathrm{ctg}^2x)=[0;\ +\infty)$

в)

$y=\sqrt{\mathrm{tg}x}$

Тангенс может принять значение любого действительного числа. Под знак корня из них можно записать любое неотрицательное, при этом в результате может получиться любое неотрицательное число.

$E(\sqrt{\mathrm{tg}x})=[0;\ +\infty)$

г)

$y=\dfrac{1}{\mathrm{ctg}x}$

Котангенс может принять значение любого действительного числа. При делении 1 на любое число (отличное от нуля) может получиться любое число, кроме нуля.

$E\left(\dfrac{1}{\mathrm{ctg}x}\right)=(-\infty;\ 0)\cup(0;\ +\infty)$