Построить график функции и описать его свойства по плану:
1. Область определения: D(f).
2. Четность, нечетность функции.
3. Монотонность (промежутки возрастания, убывания).
4. Ограниченность.
5. Наибольшее, наименьшее значение функции.
6. Непрерывность.
7. Область значения функции: E(f).
8. Периодичность.
y=cos(x-3/4п)

Показать ответ

Ответ:

Аринка20061

05.08.2020 07:30

Событие - 3 броска - независимые и, поэтому вероятности для каждого участника вычисляем по формуле:

P(A) = (p+q)³ = p³ + 3p²q + 3pq² + q³. p+q = 1.

Словами это будет как - три попадания ИЛИ 3 раза два попадания и один пром ах ИЛИ з раза одно попадание и два промаха ИЛИ три промаха.

Для первого спортсмена: p =0.6, q = 1-p = 0.4. ВАЖНО: все три промаха не учитываем.

P1(A) = 0.2166 + 0.432 + 0.288 + 0,064 - первый за 3 броска.

P2(A) = 0.343 + 0.441 + 0.189 +0,027 = 0.973 - второй за 3 броска.

Вероятность, что у первого будет больше попаданий запишем как сумму вероятностей событий (запишем в виде счета)

Р(1>2) = Р(3:2)+Р(3:1)+Р(3:0)+Р(2:1)+Р(2:0)+Р(1:0) =

= Р(3)*[Р(2)+Р(1)+Р(0)] + P(2)*[P(1)]+P(0)] + Р(1)*Р(0) =

= 0.2166*(0.441+0.189+0.027) + 0.432*(0.189+0.027) + 0.288*0.027 =

= 0.1423062 + 0.093312 + 0.00778 = 0.24333942 ≈ 0.243 - ОТВЕТ

0,0(0 оценок)

Ответ:

Незнаюзачемтутник

05.08.2020 07:30

А - попадание первого баскетболиста

В - попадание второго баскетболиста.

Имеем три случая

1) Если у первого баскетболиста три попадания, а у второго меньше 3 попадания

$P_1(A)=C^3_3p^3q^0=p^3=0.6^3=0.216\\ P_1(B)=1-p^3=1-0.7^3=0.657$

Вероятность того, что у первого баскетболиста три попадания,а у второго меньше трех попадания, равна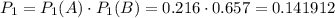 $P_1=P_1(A)\cdot P_1(B)=0.216\cdot0.657=0.141912$

2) Если у первого баскетболиста 2 попадания, а у второго 0 или 1.

$P_2(A)=C^2_3p^2q=3p^2(1-p)=3\cdot0.6^2\cdot0.4=0.432\\ P_2(B)=q^3+C^1_3pq^2=0.3^3+3\cdot0.7\cdot0.3^2=0.216$

По теореме умножения, вероятность того, что первый баскетболист попадет 2 раза, а второй - 0 или 1, равна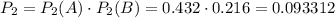 $P_{2}=P_2(A)\cdot P_2(B)=0.432\cdot0.216=0.093312$