Построить график функции

( y= -x, если x< 2

( y= 1, если -2
( x, если x> 0
это одна функция

Х = 3

Объяснение:

Сначала раскрываем скобки

Далее иксы (Х) влево, цифры вправо, когда что-то в другую сторону переставляем, знак плюс или минус меняем. Далее складываем, все по классике.

(Х+2)(4-Х)

-2Х + 6 = 0 - два икса дают 2х

-2х = -6 - минус шесть потому что переместили за знак равно, если бы икс находился за знаком равно и его бы поставили перед знаком равно, то у него был бы плюс (если изначально был минус)

Теперь, так как ввезде! минусы, то мы меняем все на плюсы (так можно только в таких случаях)

2Х = 6

Х = 3

2/3; 2

Объяснение:

3y^2-8y+4=0

D=(-8)^2-4*3*4=64-48=16

В уравнении 2 корня, значит

x1 = (-(-8) +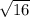 )/(2*3) = 12/6 = 2 - первый корень

x2 = (-(-8) -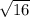 )/(2*3) = 4/6 = 2/3 - второй корень

Как найти дискриминант?

1) Дискриминант квадратного уравнения ax^2+bx+c находится по формуле: b^2-4ac. a; b и c - коэффициенты. В данном случае a=3; b=-8; c=4.

2) Подставляем: D=(-8)^2-4*(3*4)=64-48=16

3) Если D>0, то в уравнении 2 корня, если D=0, то в уравнении 1 корень, если D<0, то в уравнении корней нет

Как найти корни?

Опять же таки берём уравнение вида ax^2+bx+c

Если D>0, то x1 = (-b+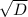)/2a

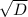                      x2 = (-b-)/2a

Если D=0, то x = -b/2a

Если D<0, то ничего не ищем

P.S. Также есть теоремы Виета и выделения полного квадрата, но они более замороченные. Конечно, проще решать через дискриминант, но если вы хотите увидеть, как решить уравнение другим напишите, я отредактирую ответ, попробую решить другим