Для того, чтобы число составленное из цифр 0, 2, 4, 7, 8 было нечетным, то последнее цифра должна быть 7 так как по признаку делимости числа на 2, то число делится на два если его последняя цифра делится на 2, а так как 0, 2, 4, 8 делится на 2, а 7 - не делится, то последняя цифра числа 7.
На оставшиеся места претендуют комбинации из цифр: 0, 2, 4, 8
Нужно выбрать 2 числа из 4 цифр, так как по условие число трехзначное. Число размещений:
Выбрать 1 элемент из трех возможно , так как ноль не может стоять на первом месте. Пусть всего составить различные нечетные трехзначных числа без повторений цифр, тогда .
3) [4/3; 3]
Объяснение:
Решение 3 неравенства
(x + 2) / (3 - x) > 2
(x + 2) / (3 - x) - (6 - 2x) / (3 - x) > 0
(x + 2 - 6 + 2x) / (3 - x) > 0
(3x -4) / (3 - x) > 0
Это неравенство больше нуля, в 2 случаях
1) когда числитель и знаменатель одновременно больше нуля
2) когда числитель и знаменатель одновременно меньше нуля
Найдем X для первого случая
3x - 4 > 0 => x > 4/3
3 - x > 0 x < 3
Т.е для 1 случая ответ от x принадлежит отрезку от [4/3; 3]
Найдем X для 2 случая
3x - 4 < 0 => x < 4/3
3 - x < 0 x > 3
Т.е для этого случая ответа нет, потому что x > 3 и x < 4/3 не могут выполняться
Поэтому ответ [4/3; 3]
Объяснение:
Для того, чтобы число составленное из цифр 0, 2, 4, 7, 8 было нечетным, то последнее цифра должна быть 7 так как по признаку делимости числа на 2, то число делится на два если его последняя цифра делится на 2, а так как 0, 2, 4, 8 делится на 2, а 7 - не делится, то последняя цифра числа 7.
На оставшиеся места претендуют комбинации из цифр: 0, 2, 4, 8
Нужно выбрать 2 числа из 4 цифр, так как по условие число трехзначное. Число размещений:
Выбрать 1 элемент из трех возможно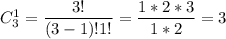
, так как ноль не может стоять на первом месте. Пусть всего составить различные нечетные трехзначных числа без повторений цифр, тогда 
.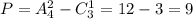