Построй её пораболу y=-x^2+4 и прямую y=x-2 и найдите координаты точек пересечения этих графиков. ​

Нам нужно доказать что одно число делиться на другое. Что из себя представляет действие деления? Это значит разложить число на два множителя, одно из которых - делитель а другое - частное. Т.е. Если число 156 делиться на 2, то его можно поделить на множители:
156:2=78
Значит раскладываем 156 на 2 и 78.
Так же в свою очередь можно разложить и 78:
78=2*39
А это значит что и число 156 можно представить в виде:
156=2*2*39
 отсюда можно сделать выводы, что число 156 делиться и на 2, и на 4, и на 78, и на 39. Вот такая логика.
Теперь рассмотрим наше число. Разложим по формуле как сумма кубов:
Сама формула: 
В нашем случае:

И давайте посмотрим на первый множитель:
36+63=99
А 99 отлично делиться на 11:
99:11=9
А это значит, что данное число () без проблем делиться на 11.

(см. объяснение)

Объяснение:

Самый верный решить любой параметр - это постараться построить его в координатах (b; x).

Попробуем применить этот прием здесь.

Сначала заметим, что при равенство неверно при любом значении параметра. Тогда на протяжении решения при необходимости будем спокойно делить на .

Раскроем :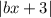

Видим гиперболу в координатах (b; x).

Построим ее и просчитаем знаки в областях, которые она образует, подставляя координаты соответствующих точек в .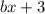

Тогда при :

Строим фрагмент этого графика в определенных выше областях.

При :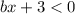

Тоже строим фрагмент этого графика в определенных выше областях.

Получим график уравнения:

(см. прикрепленный файл)

Итого:

При уравнение не имеет корней.При уравнение имеет единственный корень.При уравнение имеет ровно два различных корня.

Задание выполнено!