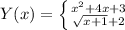Построй график данной функции. При него найди интервалы возрастания и убывания, экстремумы ( максимумы и минимумы ) функции, наибольшее и наименьшее значения функции интервалы знакопостоянства функции, чётность, нули функции и точки пересечения с осями Х и У. Х=(-5/0) 
2) a3+a8+a10+a16+a18+a23=126,найдите сумму первых 25 членов an
a3 = a1 + 2d, a8 = a1 + 7d, a10 = a1 + 9d, a16 = a1 + 15d, a18 = a1 + 17d, a23 = a1 + 22d
a1*6 + 22d + 17d + 15d + 9d + 7d + 2d = a1*6 + 40d + 17d + 15d = a1*6 + 55d + 17d = a1*6 + 72d = 126
a1 + 12d = 21, a13 = 21
a1 = a13 - 12d
a2 = a13 - 11d
a3 = a13 - 10d
...
a12 = a13 - 1d
...
a14 = a13 +1d
...
a23 = a13 +10d
a24 = a13 + 11d
a25 = a13 + 12d
S_25 = a1 + a2 + a3 + ... + a23 + a24 + a25 = 25*a13 -12d -11d -10d - ... -d + d + ... + 10d + 11d + 12d = 25*a13 = 25*21 = 525
вероятность, что будет выбрано число меньшее или равно 400
вероятность выпадения трехзначного числа до 400
(400-99)/(999-99)=0,3344 (приблизительно)
вероятность выпадения числа, делящееся на 4, но не делящееся на 8:
(76/2)/301 = 0,126 (приблизительно)
вероятность, что будет выбрано число меньшее или = 400 и делящееся на 4, но не делящееся на 8
0,3344*0,126 = 0,0422 (приблизительно)
вероятность, что будет выбрано число меньшее 400
вероятность выпадения трехзначного числа до 400
(399-99)/(999-99) = 1/3
вероятность выпадения числа, делящееся на 4, но не делящееся на 8:
(75/2)/300 = 0,125
вероятность, что будет выбрано число меньшее 400 и делящееся на 4, но не делящееся на 8
0,125/3 = 0,041667 (приблизительно)