Построй график функции y=x и по графику определи координаты точки пересечения графика функции с осью Oy.
1) Заполни таблицу.
2) Используя таблицу, построй график функции и сравни его с данным в шагах решения.
3) Определи координаты точки пересечения с осью Oy.
1) Таблица:
x -1 0 1
y
2) График.
3) Точка пересечения с осью Oy:
(;).
Дано:
х : у = 2 : 7
у : z = 9 : 10
Для того, чтобы число у приняло равные значения в обоих соотношениях, мы в первом соотношении каждое из чисел умножим на 9, а во втором соотношении каждое из чисел умножим на 7.
х : у = 2 : 7 = 18 : 63
у : z = 9 : 10 = 63 : 70
Теперь объединив в общее соотношение, получим:
x : y : z = 18 : 63 : 70
Отсюда:
x = 18
y = 63
z = 70
А теперь подставляем эти значения и находим искомые соотношения:
a) x : z = 18:70
Сократив на 2, получим:
x : z = 9 : 35 - это ответ.
б)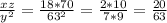
xz/y² = 20 : 63
в)(x+z)/(y+z) = 88/133
Под г) (x-z) - отрицательно, возможно в условии ошибка.
Заметим, что если раскрывать скобки в выражении (a + b)^n, то получится (a^n + n a^(n - 1) b + ...) + b^n — разложение по биному Ньютона, где каждое слагаемое в скобках делится на a. Значит, (a + b)^n даёт такой же остаток при делении на a, что и b^n.
Используем это наблюдение. Представим выражение в виде (17 + 3)^n + (17 - 1)^n - 3^n - 1. По написанному выше это выражение даёт такой же остаток при делении на 17, что и 3^n + (-1)^n - 3^n - 1 = (-1)^n - 1. Для нечётных n последнее выражение равно -2, для чётных — 0. Значит, выражение делится на 17 при чётных n и не делится при нечётных.
Тот же трюк с делимостью на 19: (19 - 1)^n + (19 - 3)^n - 3^n - 1 ≡ (-1)^n + (-3)^n - 3^n - 1. Нечётные n нас уже не интересуют, а при чётных n последнее выражение равно 0, так что исходное выражение делится на n.
Суммируем: выражение делится на 323 при чётных n (и только при таких n). Значит, подходят n = 0, 2, 4, Седьмое число в этом ряду равно 12.
ответ. 12.