Для решения задачи нужно знать, что соответствует радианам.
1) Углы равнобедренного прямоугольного треугольника равны , и (один угол - - задан в задаче, а остальные два находятся по теореме о сумме углов треугольника: ).
(представляем в виде ) - это радиан;
(уже встречалось) - радиан;
(или ) - это радиан.
2). Так как сумма углов треугольника равна (), то если все углы равны, каждый из них равен (это следует из того, что у треугольника три угла).
3). Все углы прямоугольника (таковых имеется четыре) равны. А сумма углов прямоугольника, как и любого четырехугольника, равна или радиан. Значит, каждый угол равен радиан.
1) π / 4, π / 4, π / 2;
2) π / 3, π / 3, π / 3;
3) π / 2, π / 2, π / 2, π / 2.
Для решения задачи нужно знать, что1) Углы равнобедренного прямоугольного треугольника равны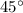 ,
, 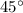 и
и 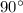 (один угол -
(один угол - 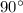 - задан в задаче, а остальные два находятся по теореме о сумме углов треугольника:
- задан в задаче, а остальные два находятся по теореме о сумме углов треугольника: 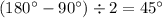 ).
).
2). Так как сумма углов треугольника равна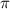 (
(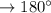 ), то если все углы равны, каждый из них равен
), то если все углы равны, каждый из них равен 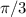 (это следует из того, что у треугольника три угла).
(это следует из того, что у треугольника три угла).
3). Все углы прямоугольника (таковых имеется четыре) равны. А сумма углов прямоугольника, как и любого четырехугольника, равна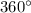 или
или 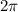 радиан. Значит, каждый угол равен
радиан. Значит, каждый угол равен 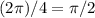 радиан.
радиан.
Или можно сразу сказать, что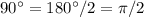 .
.
а) 1/х - 4/(х-1) = 1
1 · (х - 1) - 4 · х = 1 · х · (х - 1)
х - 1 - 4х = х² - х
х² - х - х + 1 + 4х = 0
х² + 2х + 1 = 0
D = b² - 4ac = 2² - 4 · 1 · 1 = 4 - 4 = 0
Так как дискриминант равен 0, то уравнение имеет только один корень
х = -2/(2·1) = - 2/2 = - 1
ответ: (-1).
г) 7/(х+4) + х = 4
7 + х · (х + 4) = 4 · (х + 4)
7 + х² + 4х = 4х + 16
х² + 4х - 4х - 16 + 7 = 0
х² - 9 = 0
х² - 3² = 0
(х - 3) · (х + 3) = 0
х - 3 = 0 и х + 3 = 0
х = 3 и х = - 3
Или через дискриминант
D = b² - 4ac = 0² - 4 · 1 · (-9) = 0 + 36 = 36
х₁ = (0-√36)/(2·1) = (0-6)/2 = - 6/2 = - 3
х₂ = (0+√36)/(2·1) = (0+6)/2 = 6/2 = 3
ответ: 3 и (-3).