2) Для постройки окружности на координатной прямой нужно уравнение:
;
где x; y - соответственные переменные; R - радиус.
При добавлении определённой точки в 1 четверти координатной плоскости, нужно вычесть координаты точки окружности(2;5); также у нас дан радиус 2.
Тем самым, мы получаем:
ответ:
3) Нарисовав треугольник на координатной плоскости, можно заметить, что у треугольник две стороны явно являются диагоналями прямоугольников 1x4. Так как прямоуголники равны, то и дагонали в них тоже равны => треугольник равнобедреный. (ч. и т. д.)
1) Выведем y из этих функций:
5y = 1 - 9x
y = (1-9x) / 5
3y = 8 - 2x
y = (8 - 2x) / 3
Приводим равенства и решаем уравнение:
(1 - 9x) / 5 = (8 - 2x) / 3
3(1 - 9x) = 5(8 - 2x)
3 - 27x = 40 - 10x
-37 = 17x
x = - 37/17 => y = 54/85
ответ: ( -37/17; 54/85 ).
2) Для постройки окружности на координатной прямой нужно уравнение:
где x; y - соответственные переменные; R - радиус.
При добавлении определённой точки в 1 четверти координатной плоскости, нужно вычесть координаты точки окружности(2;5); также у нас дан радиус 2.
Тем самым, мы получаем:
ответ: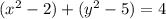
3) Нарисовав треугольник на координатной плоскости, можно заметить, что у треугольник две стороны явно являются диагоналями прямоугольников 1x4. Так как прямоуголники равны, то и дагонали в них тоже равны => треугольник равнобедреный. (ч. и т. д.)
(>= больше либо равно,<= меньше либо равно, ^ - степень, D - дискриминант)
Нужно найти наибольшее значение n.
Для этого в формулу k = m*n, подставим значение m = 140 - 10n.
Получаем, k=n*(140-10n). По условию задачи выручка, т.е. k должна быть больше или равна 450. Отсюда, n*(140 - 10n)>=450, раскрываем скобки.
- 10*n ^2 + 140*n >= 450 (переносим 450 в левую часть, и делим на (-10), получаем
n^2 - 14*n + 45 <= 0
D = 196-4*45=196-180=16
n1=(14-4)/2=5
n2=(14+4)/2=9
Наибольший корень n2, равный 9.
ответ 9.