Условие. сумма второго и восьмого членов бесконечно убывающей геометрической прогрессии равна.325/128, а сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой же прогрессии. Найти первый член прогрессии и знаменатель.
Сумма второго и восьмого членов:
Сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой прогрессии:
Из равенства заметим, что второй множитель можно разложить на множители по формуле суммы кубов
Условие. сумма второго и восьмого членов бесконечно убывающей геометрической прогрессии равна.325/128, а сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой же прогрессии. Найти первый член прогрессии и знаменатель.
Сумма второго и восьмого членов: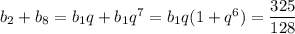
Сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой прогрессии:
Из равенства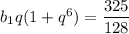 заметим, что второй множитель можно разложить на множители по формуле суммы кубов
заметим, что второй множитель можно разложить на множители по формуле суммы кубов
Подставляем данные, получим
ответ: 5; 0.5 и -5; -0.5.
=21*(-sin45)*(-sin45)=21*(sin45)^2=21*(1/√2)^2=21/2
2) tg225*sin780*cos870=tg(180+45)*sin(720+60)*cos(720+180-30)=
=tg45*sin60*(-cos30)=1*√3/2*(-√3/2)=-3/4
3) 100*sin(-5pi/4)*cos(-11pi/4)=100*(-sin(π+π/4))*cos(2π+3π/4)=
=-100*(-sinπ/4)cos(π-π/4)=100sinπ/4*(-cosπ/4)=-100*1√2*1√2=-50
4)√150*ctg(17π+π/3)*sin(15π+π3)=√25*6*ctg(π+π/3)*sin(π+π/3)=
=5√6*ctgπ/3*(-sinπ/3)=-5√6*cosπ/3=-5√6/2
Синус - нечетная функция
Косинус - четная
Целое число оборотов везде отбрасывается