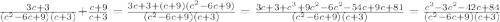Постройте график функции y=8/х
запишите свойства функции у=к/х

Показать ответ

Ответ:

софия725

14.04.2022 07:47

Пусть 10 чисел имели вид x, x + 1, ..., x + 9. Их сумма равна 10x + 45.

Вычеркивая разные числа, можно получить разные суммы.
- Наименьшая сумма получится, если вычеркнуть наибольшее число x + 9, тогда
(10x + 45) - (x + 9) <= 2015
9x + 36 <= 2015
9x <= 1979
x <= 219
- Наибольшая сумма получится, если вычеркнуть наименьшее число x, тогда
(10x + 45) - x >= 2015
9x + 45 >= 2015
9x >= 1970
x >= 219

Итак, x = 219. Сумма десяти чисел равна 10x + 45 = 2235, а вычеркнутое число 2235 - 2015 = 220

0,0(0 оценок)

Ответ:

Parade93

26.06.2022 19:53

$\frac{c^{3}-3c^{2}-42c+84}{(c^{2}- 6c+9)(c+3)}$

Объяснение:

$(\frac{1}{c^{2} - 9} + \frac{1}{c^{2} - 6c + 9} )+\frac{1}{(3-c)^{2}} + \frac{c+9}{c+3}$

Это задание в первую очередь ориентировано на проверку ваших знаний ФСУ или Формул Сокращённого Умножения.

Давайте просканируем пример на их наличие.

1.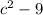 $c^{2} - 9$ - Это разность квадратов, а именно квадрата числа с и числа 3. Возможно вы зададите резонный вопрос - а зачем нам это отслеживать. В работе с дробями важно уметь находить взаимосвязи между знаменателями. 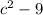$c^{2} - 9$ раскладывается рак (с-3)(с+3)

2.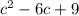 $c^{2} - 6c + 9$ - знаменатель второй дроби и является квадратом разности(смотрим по знаку перед вторым числом). Он раскладывается как (с-3)(с-3).

Что-то напоминает не так ли? Таким образом, с-3 это общий множитель обоих знаменателей. Значит нужно перемножит каждую дробь на оставшийся общий множитель другой дроби

$\frac{1}{c^{2} - 9} + \frac{1}{c^{2}-6c+9} = \frac{c-3}{(c^{2}-9)(c-3)} + \frac{c+3}{(c^{2}-6c+9)(c+3)} =\frac{2c}{(c-3)(с-3)(c+3)}$

Я специально оставила дробь полностью раскрытой, т.к. она нам ещё может понадобиться.

3.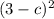 $(3-c)^{2}$ - аналогично пункту 2 квадрат разности. Раскладывается практически аналогично. Но т.к. от перемены мест слагаемых сумма не меняется это исправимо.

$\frac{2c}{(c-3)(c-3)(c+3)}+ \frac{1}{9 - 6c+c^{2}} = \frac{2c+c+3}{(c^{2}-6c+9)(c+3)}=\frac{3c+3}{(c^{2}-6c+9)(c+3)}$

Дальше приведём получившуюся дробь и оставшуюся к общему знаменателю. $\frac{3c+3}{(c^{2}-6c+9)(c+3)} + \frac{c+9}{c+3} = \frac{3c+3+(c+9)(c^{2}-6c+9)}{(c^{2}- 6c+9)(c+3)} = \frac{3c+3+c^{3}+ 9c^{2}-6c^{2} - 54c+9c+81}{(c^{2}- 6c+9)(c+3)} = \frac{c^{3}-3c^{2}-42c+84}{(c^{2}- 6c+9)(c+3)}$