ответ: плотность водорода равна "ро" = 81 г/м куб.
Объяснение:
Задача. Дано: водород, t = 15 град С; p = 730 мм Hg ; Определить плотность "ро" - ?Решение. Запишем уравнение Клапейрона - Менделеева. pV = mRT/M; плотность равна "ро"= m/V ; поэтому разделим левую и правую часть равенства на V . Потом заменим отношение m/V = "ро", получим р = "ро"*RT/M, откуда "ро" = pM/RT; Для вычислений все величины надо выразить в СИ. 1 мм Hg = 133 Па; р = 730 мм Hg = 730*133 = 97090 Па; T = t + 273; Т = 15 + 273 = 288 (К) . Из таблиц М = 2*10(в минус 3 ст) кг/моль; R = 8,31 Дж/кг* К; А теперь подставим: "ро" = (97090 Па*2*10( в минус 3 ст) кг/моль) / (8,31 Дж/моль*К * 288 К) = 0,081 кг/ м куб = 81 г/м куб.
Пусть одно из слагаемых равно x. Тогда второе равно 5-x. Произведение, о котором говорится в условии задается формулой . Нам нужно найти x, для которого это выражение оказывается наибольшим. То есть фактически нужно найти точку максимума функции на интервале (0; 5).
Возьмём производную:
На заданном интервале производная имеет единственный ноль: точку x=1. При этом: f(0)=f(5)=0, f(1)=256. Значит x=1 - точка максимума на интервале (0; 5).
1 это первое слагаемое. Тогда второе, очевидно, равно 4.
ответ: плотность водорода равна "ро" = 81 г/м куб.
Объяснение:
Задача. Дано: водород, t = 15 град С; p = 730 мм Hg ; Определить плотность "ро" - ?Решение. Запишем уравнение Клапейрона - Менделеева. pV = mRT/M; плотность равна "ро"= m/V ; поэтому разделим левую и правую часть равенства на V . Потом заменим отношение m/V = "ро", получим р = "ро"*RT/M, откуда "ро" = pM/RT; Для вычислений все величины надо выразить в СИ. 1 мм Hg = 133 Па; р = 730 мм Hg = 730*133 = 97090 Па; T = t + 273; Т = 15 + 273 = 288 (К) . Из таблиц М = 2*10(в минус 3 ст) кг/моль; R = 8,31 Дж/кг* К; А теперь подставим: "ро" = (97090 Па*2*10( в минус 3 ст) кг/моль) / (8,31 Дж/моль*К * 288 К) = 0,081 кг/ м куб = 81 г/м куб.
Пусть одно из слагаемых равно x. Тогда второе равно 5-x. Произведение, о котором говорится в условии задается формулой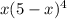
. Нам нужно найти x, для которого это выражение оказывается наибольшим. То есть фактически нужно найти точку максимума функции 
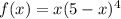на интервале (0; 5).
Возьмём производную:
На заданном интервале производная имеет единственный ноль: точку x=1. При этом: f(0)=f(5)=0, f(1)=256. Значит x=1 - точка максимума на интервале (0; 5).
1 это первое слагаемое. Тогда второе, очевидно, равно 4.
ответ: 1 и 4